Page 115 - 2024年第55卷第8期

加 ０．０５７ＭＰａ、压应力增加 １．１７５ＭＰａ（有限元法和解析法结果的平均值），因此，在体积变化一定的条
件下，拱曲率半径对应力的影响程度显著大于拱厚度。反之，若要降低 １ＭＰａ拉应力，通过减小曲率
３
３
半径的方式需要增加约 １４００ｍ 混凝土，通过增加厚度的方式需要增加约 ３５００ｍ 混凝土，约为前者的
３
２．５倍；若要降低 １ＭＰａ压应力，通过减小曲率半径的方式需要增加约 ２１ｍ 混凝土，通过增加厚度的
３
方式需要增加约 １７０ｍ 混凝土，约为前者的 ８．５倍。这一差异将成为后续优化迭代算法的核心依据。
表 ２ 不同曲率半径和拱厚度条件下的应力极值

单位高度 曲率半径 拱厚度 最大拉应力 最大压应力 单位高度 曲率半径 拱厚度 最大拉应力 最大压应力
体积?ｍ ３ ?ｍ ?ｍ ?ＭＰａ ?ＭＰａ 体积?ｍ ３ ?ｍ ?ｍ ?ＭＰａ ?ＭＰａ
２４００ １３０．０ １０．１２ ０．０４６ １７．３４＼１６．５７ ２４００ １３０ １０．１２ ０．０４６ １７．３４＼１６．５７
２３５０ １３７．５ １０．１２ ０．０６７ １８．６９＼１７．９６ ２３５０ １３０ ９．９２ ０．０５８ １７．６２＼１６．８４
２３００ １４７．６ １０．１２ ０．０９０ ２０．５１＼１９．７８ ２３００ １３０ ９．７２ ０．０７１ １７．９１＼１７．１３
２２５０ １６２．１ １０．１２ ０．１３２ ２３．１４＼２２．３１ ２２５０ １３０ ９．５１ ０．０８９ １８．２０＼１７．４３
２２００ １８３．５ １０．１２ ０．１９２ ２７．０５＼２６．０６ ２２００ １３０ ９．３１ ０．１０３ １８．５２＼１７．７４
注：最大压应力栏两个应力值为：解析解 ＼有限元解。

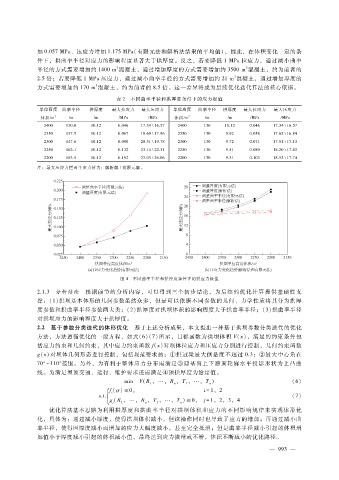
图 ４ 不同曲率半径和拱厚度条件下的拱应力极值

２．１．３ 分析结论 根据前节的分析内容，可以得到三个初步结论，为后续的优化计算提供基础性支
撑：（１）拱坝基本体形的几何参数虽然众多，但是可以依据不同参数的几何、力学性质将其分为拱厚
度参数和拱曲率半径参数两大类；（ ２）拱厚度对拱坝体积的影响程度大于拱曲率半径；（３）拱曲率半径
对拱坝应力的影响程度大于拱厚度。
２．２ 基于参数分类迭代的体形优化 基于上述分析成果，本文提出一种基于拱坝参数分类迭代的优化
方法，方法遵循优化的一般方程，如式（ ６）（７）所示，目标函数为拱坝体积 Ｖ（ｘ），满足的约束条件包
括应力约束和几何约束，其中应力约束函数 ｆ（ｘ）对坝体拉应力和压应力分别进行控制，几何约束函数
ｇ（ｘ）对坝体几何形态进行控制，包括规范要求的：①拱冠梁最大倒悬度不超过 ０．３；②最大中心角在
７０°～１１０°范围。另外，为有利于整体应力分布需满足③建基面上下游面轮廓水平投影形状为上凸曲
线。为满足坝顶交通、运行、维护要求还需满足④顶拱厚度为给定值。
ｍｉｎ Ｖ（Ｒ，…，Ｒ，Ｔ，…，Ｔ） （６）
ｎ
ｎ
１
１
{ ｆ（ σ ） ≤０， ｉ ＝ １ ，２
ｉ
ｓ．ｔ． ｇ（Ｒ，…，Ｒ，Ｔ，…，Ｔ） ≤０， ｊ ＝ １ ，２，３，４ （７）
１
ｎ
１
ｎ
ｊ
优化算法基本思路为利用拱厚度和拱曲率半径对拱坝体积和应力的不同影响规律来实现体形优
化，具体为：通过减小厚度，使得拱坝体积减小，但该操作同时也导致了应力的增加；再通过减小曲
率半径，使得因厚度减小而增加的应力大幅度减小，甚至完全抵消；但是曲率半径减小引起的体积增
加值小于厚度减小引起的体积减小值，最终达到应力微增或不增，体积不断减小的优化路径。
— ９ ９ ３ —