Page 54 - 2024年第55卷第9期

破碎规律，初步掌握了影响粗粒料破碎的主要因素。纪文栋等 ［１１］ 通过开展侧限压缩、三轴压缩、单向
剪切和循环剪切 ４种试验，研究了不同加载方式和应力水平下珊瑚砂的颗粒破碎演化规律，结果表明
不同应力加载模式对粗颗粒的破碎有着显著影响。在筑坝过程中，粗粒料受到振动冲击荷载作用下而
发生颗粒破碎，导致级配发生明显改变，这就意味着现有的研究结果对于筑坝粗粒料碾压等实际工况
并不适用。为了分析粗粒料在冲击荷载作用下颗粒破碎的变化规律及 级 配 分布，Ｘｉａｏ等 ［１２］ 、Ｗａｎｇ
等 ［１３］ 和 Ｃｈｅｎ等 ［１４］ 通过对钙质砂、石英砂开展了冲击荷载试验，研究了不同冲击能作用下钙质砂和石
英砂的颗粒破碎演化规律。上述研究虽取得了较多成果，促进了岩土颗粒破碎演变规律的认识，但仍
存在较多问题尚未解决。现有研究主要是以钙质砂、石英砂等岩土体为主，而炭质泥岩与钙质砂、石
英砂等材料的颗粒破碎难易程度有着本质区别，例如，钙质砂颗粒内部孔隙丰富、强度低，含水率对
颗粒破碎的影响并不显著 ［１２ － １４］ 。炭质泥岩在干燥状态力学良好，然而遇水易破碎、内部孔隙扩展、强
度降低。目前关于不同冲击能与含水率条件下的炭质泥岩研究亟待深入，因此有必要开展上述两种因
素共同作用下炭质泥岩颗粒破碎及其级配演变规律的研究。
综上所述，目前学者们主要研究不同应力加载模式下粗粒料的破碎规律，同时建立应力应变、冲
击能等外界因素与颗粒破碎的内在关系，但无法进一步反映级配的演化。为此郭万里等 ［１５］ 基于双参数
级配方程，提出了 “应力应变－ 破碎指标 － 级配方程” 的转换模型，该模型可较好地描述级配随应力
应变演变的规律。丁林楠等 ［１６］ 考虑到双级配参数方程在计算过程中的复杂性，基于分形级配方程，建
立了单参数 “应力应变－ 破碎指标 － 级配分布” 模型，然而分形级配方程在描述连续级配曲线时具有
一定的局限性。因此，考虑到上述两类方程在实际应用中的不足之处，本文尝试基于一个新的单参数
级配方程，建立一个关于 “冲击能和含水率 － 破碎指标 － 级配分布” 的模型，揭示炭质泥岩颗粒破碎
及级配分布随冲击能与含水率的演变规律。

２ 破碎指标与级配方程的关系

２．１ 级配方程的选择 级配不仅影响影响土体的强
度，同时也是影响土体渗透性的主要因素之一 ［１７ － １８］ 。
我国《土工试验规范》规定了土体级配良好的条件，即
［１９］
不均匀系数 Ｃ＞５、曲率系数 Ｃ ＝ １～３ 。然而，利用
ｕ ｃ
Ｃ和 Ｃ只能定性描述土体级配，不能完整地描述土
ｃ
ｕ
体级配（不 同 级 配 可 能 有 相 同 的 Ｃ、 Ｃ）。 朱 俊 高
ｃ
ｕ
等 ［２０］ 通过对大量土体级配进行分析，归纳了连续级
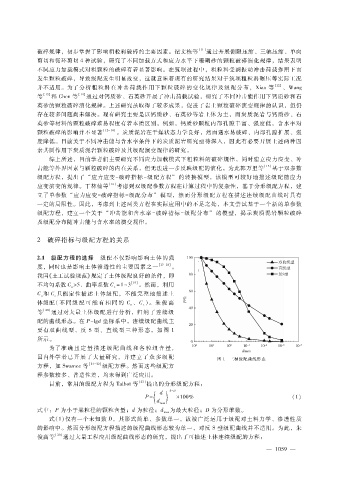
配的曲线形态。在 Ｐ － ｌｇｄ坐标系中，连续级配曲线主
要有双 曲 线 型、反 Ｓ型、直 线 型 三 种 形 态，如 图 １
所示。
为了准 确 且 定 量 描 述 级 配 曲 线 和 各 粒 组 含 量，
国内外学者已开展了大量研究，并建立了 众 多 级配 图 １ 三种级配曲线形态
方程，如 Ｓｗａｍｅｅ等 ［２１ － ２２］ 级配方程。然而这些级配方
程参数较多、普适性差，均未得到广泛应用。
目前，常用的级配方程为 Ｔａｌｂｏｔ等 ［２３］ 提出的分形级配方程：
ｄ
Ｐ ＝ ( ) ３ － Ｄ × １００ ％ （１）
ｄ
ｍａｘ
式中：Ｐ为小于某粒径的颗粒含量；ｄ为粒径；ｄ 为最大粒径；Ｄ为分形维数。
ｍａｘ
式（ １）仅有一个未知数 Ｄ，其形式简单、参数单一，故被广泛运用于级配对土料力学、渗透性质
的影响中。然而分形级配方程描述的级配曲线形态较为单一，对反 Ｓ型级配曲线并不适用。为此，朱
俊高等 ［２０］ 通过大量工程应用级配曲线形态的研究，提出了可描述土体连续级配的方程：

０
— １ ５ ９ —