Page 55 - 2024年第55卷第9期

１
Ｐ ＝ ｆ（ｂ，ｍ） ＝ ｍ × １００％ （２）
ｄ
( ) ＋ ｂ
ｍａｘ
（１ － ｂ） ｄ
式中 ｂ、ｍ为级配参数，其中 ｂ＜１且 ｍ＞０。
研究表明：式（ ２）可以较好地描述直线型、反 Ｓ型、双曲线型的级配曲线，然而由于存在多个级
配参数，土体的力学性质、渗透性质随级配参数 ｂ、ｍ的变化规律是无序的，从而导致级配参数不能
定量描述级配对土体力学、渗流性质的影响 ［１８，２４］ 。
吴二鲁等 ［２５］ 针对上述两种级配方程的不足之处，构造了如下级配方程：
１
Ｐ ＝ 槡 β × １００ ％ （３）
ｄ
( )
ｍａｘ
（１ － β ） × ｄ ＋ β
式中 β 为级配参数，其中 β 的取值范围为（０，１）。
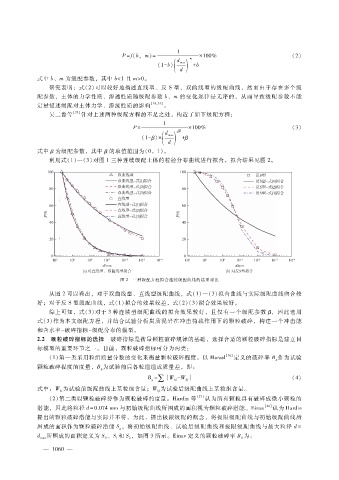
利用式（ １）—（３）对图 １三种连续级配土体的粒径分布曲线进行拟合，拟合结果见图 ２。

图 ２ 三种级配方程拟合连续级配曲线的结果对比

从图 ２可以看出，对于双曲线型、直线型级配曲线，式（１）—（３）拟合曲线与实际级配曲线吻合较
好；对于反 Ｓ型级配曲线，式（１）拟合的效果较差，式（２）（３）拟合效果较好。
综上可知，式（ ３）对于 ３种连续型级配曲线的拟合效果较好，且仅有一个级配参数 β ，因此选用
式（３）作为本文级配方程，并结合试验分析炭质泥岩在冲击荷载作用下的颗粒破碎，构建一个冲击能
和含水率－ 破碎指标－ 级配分布的模型。
２．２ 颗粒破碎指标的选择 破碎指标是衡量颗粒破碎规律的基础，选择合适的颗粒破碎指标是建立目
标模型的重要环节之一。目前，颗粒破碎指标可分为两类：
［２６］
（ １）第一类采用粒组质量分数的变化来衡量颗粒破碎程度。以 Ｍａｒａｓｌ 定义的破碎率 Ｂ作为试验
ｇ
颗粒破碎程度的度量，Ｂ为试验前后各粒组组成质量差，即：
ｇ
ｇ ∑
Ｂ ＝ Ｗ － Ｗ ｋｆ （４）
ｋｉ
式中：Ｗ 为试验前级配曲线上某粒组含量；Ｗ 为试验后级配曲线上某粒组含量。
ｋｉ ｋｆ
（ ２）第二类以颗粒破碎势作为颗粒破碎的度量。Ｈａｒｄｉｎ等 ［２７］ 认为所有颗粒具有破碎成微小颗粒的
［２８］
潜能，因此将粒径 ｄ ＝ ０．０７４ｍｍ与初始级配曲线所围成的面积视为颗粒破碎潜能。Ｅｉｎａｖ 认为 Ｈａｒｄｉｎ
提出的颗粒破碎潜能与实际并不符，为此，提出极限级配的概念，将极限级配曲线与初始级配曲线所
围成的面积作为颗粒破碎潜能 Ｓ，将初始级配曲线、试验后级配曲线和极限级配曲线与最大粒径 ｄ ＝
ｇ
ｄ 所围成的面积定义为 Ｓ、Ｓ和 Ｓ，如图 ３所示。Ｅｉｎａｖ定义的颗粒破碎率 Ｂ 为：
ｍａｘ ０ １ ２ Ｅ
６
— １ ０ ０ —