Page 56 - 2024年第55卷第9期

Ｓ－ Ｓ
０
１
Ｂ ＝ （５）
Ｅ
Ｓ－ Ｓ
２ ０
郭万里等 ［１５］ 认为颗粒破碎率 Ｂ 具有一定的局限性，主要原因是试样的级配极限曲线需要通过额
Ｅ
外试验进行确定，而且根据大量试验结果表明：试样的极限级配不仅取决于试样的初始级配、颗粒形
状、矿物成分，还因加载条件的差异而有所不同 ［１４］ 。因此，为了简化计算，郭万里等定义了一个新的
颗粒破碎指标 Ｂ ，其表达式为：
ｗ
Ｓ－ Ｓ
Ｂ ＝ １ ０ （６）
ｗ
Ｓ
０
从式（ ６）可以看出，Ｂ 的理论变化范围为 ０到无穷大，而其它颗粒破碎指标的变化范围均为 ０～１，
ｗ
因此理论上不如其它颗粒破碎指标。但是，对于给定的某种粗粒料，初始级配曲线确定 后 （ Ｓ为定
０
值），其对应的极限级配曲线也随之确定（Ｓ为定值）。对比式（５）（６）可知，二者仅是分母不同，而分
２
子 Ｓ－ Ｓ作为试验过程中的破碎量，从图 ３可以看出，其数值越大，级配曲线变化越大，颗粒破碎越
１ ０
显著，故 Ｂ 可以反映土体级配的整体变化，简单实用，不需要通过额外试验来确定炭质泥岩粗粒料的
ｗ
极限级配。因此，本文拟采用 Ｂ 作为判定粗粒土颗粒破碎的指标。
ｗ
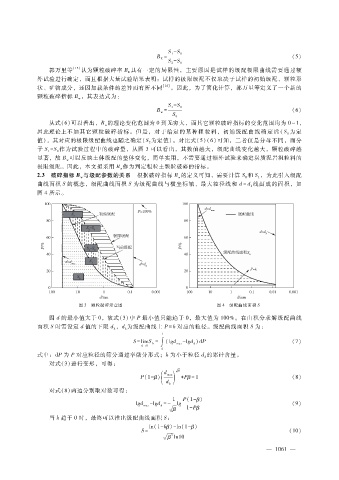
２．３ 破碎指标 Ｂ 与级配参数的关系 根据破碎指标 Ｂ 的定义可知，需要计算 Ｓ和 Ｓ，为此引入级配
ｗ ｗ ０ １
曲线面积 Ｓ的概念，级配曲线面积 Ｓ为级配曲线与横坐标轴、最大粒径线和 ｄ ＝ ｄ线围成的面积，如
ｋ
图 ４所示。

图 ３ 颗粒破碎示意图 图 ４ 级配曲线面积 Ｓ

因 ｄ的最小值大于 ０，故式（３）中 Ｐ最小值只能趋于 ０，最大值为 １００％。在由积分求解级配曲线
面积 Ｓ时需设定 ｄ值的下限 ｄ，ｄ为级配曲线上 Ｐ ＝ ｋ对应的粒径。级配曲线面积 Ｓ为：
ｋ
ｋ
１
Ａ ∫
Ｓ ＝ ｌｉｍ Ｓ ＝ （ｌｇｄ － ｌｇ ｄ）ｄＰ （７）
ｋ
ｍａｘ
ｋ → ０
ｋ
式中：ｄＰ为 Ｐ对应粒径的筛分通过率微分形式；ｋ为小于粒径 ｄ的累计含量。
ｋ
对式（ ３）进行变形，可得：
槡 β
ｄ
( ) ＋ Ｐ β ＝ １
ｍａｘ
Ｐ（１ － β ） （８）
ｄ
ｋ
对式（８）两边分别取对数可得：
１ Ｐ（１ － β ）
ｌｇｄ － ｌｇｄ＝－ ｌｇ （９）
ｍａｘ ｋ １ － Ｐ β
槡 β
当 ｋ趋于 ０时，最终可以推出级配曲线面积 Ｓ：
ｌｎ（１ － ｋ β ） － ｌｎ （１ － β ）
Ｓ ＝ （１０）
３
槡 βｌｎ１０
０
— １ ６ １ —