Page 11 - 2024年第55卷第12期

图 ７ ＣＯＶ ｃ 与 ＣＯＶ 联合作用对土石坝坝坡可靠度的影响
φ
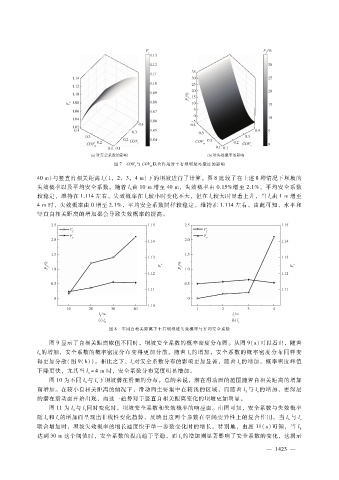
４０ｍ）与竖直自相关距离 ｌ（１，２，３，４ｍ）下的坝坡进行了计算。图 ８比较了在上述 ８种情况下坝坡的
ｖ
失效概率以及平均安全系数。随着 ｌ由 １０ｍ增至 ４０ｍ，失效概率由 ０．１５％增至 ２．１％，平均安全系数
ｈ
较稳定，维持在 １．１１４左右。失效概率在 ｌ较小时变化不大，但在 ｌ较大时显著上升，当 ｌ由 １ｍ增至
ｖ
ｖ
ｖ
４ｍ时，失效概率由 ０增至 ２．１％，平均安全系数同样较稳定，维持在 １．１１４左右。由此可知，水平和
竖直自相关距离的增加都会导致失效概率的提高。

图 ８ 不同自相关距离下土石坝坝坡失效概率与平均安全系数

图 ９显示了自相关距离取值不同时，坝坡安全系数的概率密度分布图。从图 ９（ａ）可以看出，随着
ｌ的增加，安全系数的概率密度分布变得更加分散。随着 ｌ的增加，安全系数的概率密度分布同样变
ｈ ｖ
得更加分散（图 ９（ｂ））。相比之下，ｌ对安全系数分布的影响更加显著，随着 ｌ的增加，概率密度峰值
ｖ
ｖ
下降更快，尤其当 ｌ ＝ ４ｍ时，安全系数分布宽度明显增加。
ｖ
图 １０为不同 ｌ与 ｌ下坝坡潜在滑面的分布。总的来说，潜在滑动面的范围随着自相关距离的增加
ｈ ｖ
而增加。在较小自相关距离的情况下，滑动面主要集中在较浅的区域，而随着 ｌ与 ｌ的增加，更深层
ｈ
ｖ
的潜在滑动面开始出现，而这一趋势对于竖直自相关距离变化的坝坡更加明显。
图 １１为 ｌ与 ｌ同时变化时，坝坡安全系数和失效概率的响应面。由图可知，安全系数与失效概率
ｈ ｖ
随 ｌ和 ｌ的增加而呈现出非线性变化趋势，反映出这两个参数在空间变异性上的复合作用。当 ｌ与 ｌ
ｈ ｖ ｈ ｖ
联合增加时，坝坡失效概率的增长速度快于单一参数变化时的增长。特别地，由图 １１（ａ）可知，当 ｌ
ｈ
达到 ３０ｍ这个阈值时，安全系数的提高趋于平稳，而 ｌ的增加则显著影响了安全系数的变化，这揭示
ｖ
— １ ２ ３ —
４