Page 115 - 2025年第56卷第11期

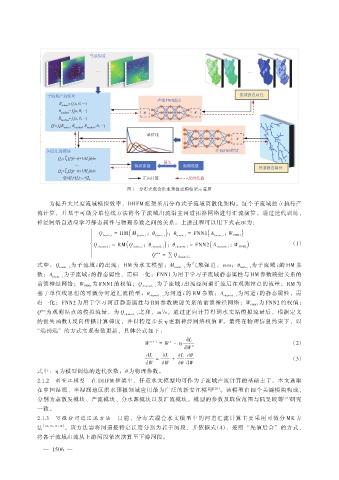
图 1 分布式混合洪水预报建模框架示意图

为提升大尺度流域模拟效率，DHFM 框架采用分布式子流域离散化架构。每个子流域独立执行产
流计算，并基于可微分单位线方法将各子流域出流沿主河道拓扑网络进行汇流演算。通过迭代训练，
神经网络自适应学习静态属性与物理参数之间的关系。上述过程可以用下式表示为：
(
(
ì Q = HM M ；θ ) ；θ = FNN1 A )
ï ï basin， i basin， i basin，i basin， i basin， i ；W FNN1
(
ï ï
(
íQ i = RM Q i ；θ i ) ；θ i = FNN2 A i ；W FNN2 ) （1）

ï ï channel， basin， channel， channel， channel，
ï ï Q sim = ∑Q channel， i
î
式中：Q basin，i 为子流域 i 的出流；HM 为水文模型；M basin，i 为气象强迫，mm；θ basin，i 为子流域 i 的 HM 参
数；A basin，i 为子流域 i 的静态属性，需归一化；FNN1 为用于学习子流域静态属性与 HM 参数映射关系的
前馈神经网络；W 为 FNN1 的权值；Q 为子流域 i 出流经河道汇流后在观测站点的流量；RM 为
FNN1 channel，i
基于单位线思想的可微分河道汇流模型；θ channel，i 为河道 i 的 RM 参数；A channel，i 为河道 i 的静态属性，需
归一化；FNN2 为用于学习河道静态属性与 RM 参数映射关系的前馈神经网络；W 为 FNN2 的权值；
FNN2
Q 为观测站点的模拟流量，为 Q channel，i 之和，m /s。通过正向计算得到水文站模拟流量后，根据定义
3
sim
的损失函数 L 反向传播计算梯度，并以特定步长 η 更新神经网络权值 W。最终在物理信息约束下，以
“端到端”的方式实现参数更新，具体公式如下：
dL
W n + 1 = W - η （2）
n
dW n
dL ∂L ∂L dθ
dW = ∂W + ∂θ dW （3）
式中：η 为模型训练的迭代次数；θ 为物理参数。
2.1.2 新安江模型 在 DHFM 框架中，任意水文模型均可作为子流域产流计算的基础主干。本文选取
在中国湿润、半湿润地区洪水预报领域应用最为广泛的新安江模型 ［20］ 。该模型由四个关键模块构成，
分别为蒸散发模块、产流模块、分水源模块以及汇流模块。模型的参数及取值范围与陆旻皎等 ［21］ 研究
一致。
2.1.3 可微分河道汇流方法 目前，分布式混合水文模型中的河道汇流计算主要采用可微分 MK 方
法 ［14-15，17-18］ 。该方法需将河道按特定长度分割为若干河段，并依据式（4），按照“先演后合”的方式，
将各子流域出流从上游河段依次演算至下游河段。

— 1506 —