Page 120 - 水利学报2021年第52卷第1期

W - W
H = 1 2 （8）
2BΔx
上式中，令 ΔW = W - W 表示高低流量期间下泄的水量差值，令 S = BΔx 表示水库响应段的表面积，
1 2
同时采用水位波动的振幅 A = H/2 带入上式，可得：
A = ΔW （9）
4S
η
上式中水库响应段表面积 S 与背景水位 ( ) 相关，假定二者之间呈线性关系，令：
S = a ⋅ η + b （10）
1 1
将式（10）带入式（9），并合并待定系数，可得振幅与泄流水量差（ ΔW ）和背景水位（η）之间的表达
式为：

A = ΔW （11）
a ⋅ η + b
)
通过三峡大坝的实测出库流量和秭归站的波高，可通过拟合求得待定系数 (a，b ，从而得到坝前水
位振幅估算公式：
A = DW ´ 10 -7 （12）
2.34 ⋅ η - 260.24
需要说明的是，由于推导过程中假定水位与面积呈线性关系，导致方程（11）两端量纲不对等。公式
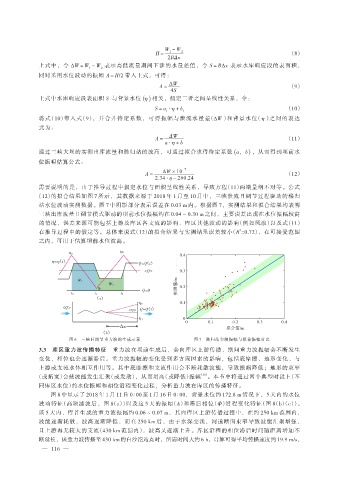
（12）的拟合结果如图 7 所示，其数据来源于 2018 年 1 月至 10 月中，三峡泄流日调节过程驱动的秭归
站水位波动实测数据。图 7 中阴影部分表示误差在 0.03 m 内。根据图 7，实测结果和拟合结果均表明
三峡出库流量日调节模式驱动的坝前水位振幅约在 0.04 ~ 0.30 m 之间，主要误差出现在水位振幅较高
的情况，误差来源可能包括上游及库区各支流的影响、库区其他波动的影响（例如风浪）以及式（11）
2
在推导过程中的假定等。总体来说式（12）的拟合结果与实测结果误差较小（R =0.72），在可接受范围
之内，可用于估算坝前水位波高。

η 0
η 0
0.4
η=η（t） Q=Q（t）
<Q> 0.3
实测值/m 0.2
W 1
W 2
η 1
Q=0
t 0 t 1 t 2
（a）
0.1
η 0
<Q>
<η> Q=Q（t）
η 1 0
Δx 0 0.1 0.2 0.3 0.4
拟合值/m
（b）
图 6 三峡日调节重力波的生成示意 图 7 秭归站实测振幅与拟合振幅对比
3.3 库区重力波传播特征 重力波在坝前生成后，会向库区上游传播，期间重力波振幅会不断发生
变化，相位也会逐渐滞后。重力波振幅的变化受到多方面因素的影响，包括底摩擦、地形变化、与
上游或支流水体相互作用等。其中底摩擦和支流作用会不断耗散波能，导致振幅降低；地形的束窄
（或拓宽）会使波能发生汇聚（或发散），从而增高（或降低）振幅 ［20］ 。本节中将通过两个典型时段上（不
同库区水位）的水位振幅和相位沿程变化过程，分析重力波在库区的传播特征。
图 8 中显示了 2018 年 1 月 11 日 0∶00 至 1 月 16 日 0∶00，背景水位约 172.8 m 情况下，5 天内的水位
波动特征（高频滤波后，图 8（a））以及这 5 天的振幅（A）和滞后相位（Φ）沿程变化特征（图 8（b）（c））。
该 5 天内，库首生成的重力波振幅约 0.06 ~ 0.07 m，其向库区上游传播过程中，在约 250 km 范围内，
波能逐渐耗散，波高逐渐降低，而在 250 km 后，由于水深变浅，河道断面束窄导致波能汇聚增强，
且上游再无较大的支流（430 km 范围内），波高又逐渐上升。库区沿程的相位滞后时间随距离增加不
断延长，该重力波传播至 430 km的白沙沱站点时，所需时间大约 6 h，计算可得平均传播速度约 19.9 m/s，
— 116 —