Page 119 - 水利学报2021年第52卷第1期

（万 m 3 /s）

流量/

时间（时/日）
（a）日调节，2018 年 5 月
（万 m 3 /s）

流量/

时间（时/日）
（b）半日调节，2018 年 9 月

（万 m 3 /s）

流量/

时间（时/日）
（c）平稳调度，2018 年 8 月

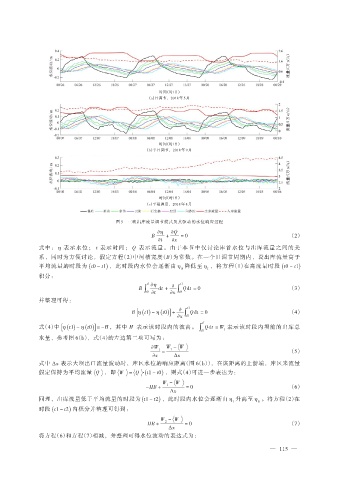
图 5 三峡出库流量调节模式及其驱动的水位响应过程
∂η ∂Q
B + = 0 （2）
∂t ∂x
式中： η 表示水位； t 表示时间； Q 表示流量。由于本节中仅讨论库首水位与出库流量之间的关
系，同时为方便讨论，假定方程（2）中河槽宽度（B）为常数。在一个日调节周期内，设出库流量高于
)
平均流量的时段为 (t0 ~ t1 ，此时段内水位会逐渐由 η 降低至 η ，将方程（1）在高流量时段 (t0 ~ t1 )
0 1
积分：
t1 ∂η t1
B dt + ∂ Qdt = 0 （3）
 t0 ∂t ∂x  t0
并整理可得：
]
B [ η ( ) - η ( ) + ∂ t1 Qdt = 0 （4）
t1
t0
∂x  t0
]
式（4）中 [ η ( ) - η ( ) = -H ，其中 H 表示该时段内的波高。 t1 Qdt = W 表示该时段内坝前的出库总
t0
t1
 t0 1
水量，参考图 6（b），式（4）的左边第二项可写为：
∂W W - W
1 = 1 （5）
∂x Δx
式中 Δx 表示大坝出口流量波动时，库区水位的响应距离（图 6（b）），在该距离的上游端，库区来流量
)
假定保持为平均流量 Q ，即 W = Q · (t1 - t0 ，则式（4）可进一步表达为：
W - W
-HB + 1 = 0 （6）
Δx
)
同理，出库流量低于平均流量的时段为 (t1 - t2 ，此时段内水位会逐渐由 η 升高至 η 。将方程（2）在
1 0
)
时段 (t1 - t2 内积分并整理可得到：
W - W
HB + 2 = 0 （7）
Δx
将方程（6）和方程（7）相减，并整理可得水位波动的表达式为：

— 115 —