Page 105 - 水利学报2021年第52卷第3期

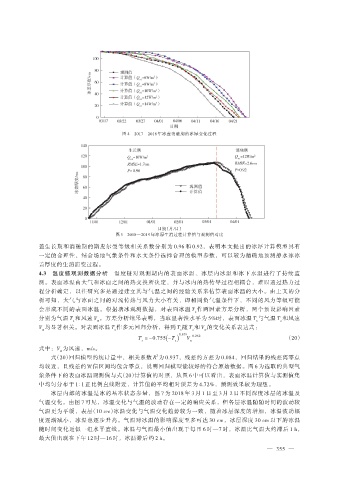
图 4 2017—2018 年冰盖消融期的冰厚变化过程

日期（月/日）
图 5 2018—2019 年冰厚生消过程计算值与观测值对比
盖生长期和消融期的斯皮尔曼等级相关系数分别为 0.96 和 0.92，表明本文提出的冰厚计算模型具有
一定的合理性，结合场地气象条件和水文条件选择合理的模型参数，可以较为精确地预测静水冰冰
盖厚度的生消演变过程。
4.3 温度链观测数据分析 温度链对观测期内的表面冰温、冰层内冰温和冰下水温进行了持续监
测。表面冰温由大气和冰面之间的热交换所决定，并与冰内的热传导过程相耦合，难以通过热力过
程分析确定，以往研究多是通过建立其与气温之间的经验关系来估算表面冰温的大小。由上文的分
析可知，大气与冰面之间的对流传热与风力大小有关，即相同负气温条件下，不同的风力等级可能
会形成不同的表面冰温。根据塘冰观测数据，对表面冰温 T 作两因素方差分析，两个预设影响因素
s
分别为气温 T 和风速 V 。方差分析结果表明，当取显著性水平为 5%时，表面冰温 T 与气温 T 和风速
a w s a
V 均显著相关。对表面冰温 T 作多元回归分析，得到 T 随 T 和 V 的变化关系表达式：
w s s a w
T = -0.755(-T ) 0.679 V 0.262 （20）
s a w
式中：V 为风速，m/s。
w
2
式（20）回归模型的统计量中，相关系数 R 为 0.937，残差的方差为 0.084，回归结果的残差离零点
均较近，且残差的置信区间均包含零点，说明回归模型能较好的符合原始数据。图 6 为选取的典型气
象条件下的表面冰温观测值与式（20）计算值的对照，从图 6 中可以看出，表面冰温计算值与实测值集
中均匀分布于 1∶1 正比例直线附近，计算值的平均相对误差为 4.72%，预测效果较为理想。
冰层内部的冰温是冰的基本状态参量，图 7 为 2018 年 3 月 1 日至 3 月 2 日不同深度冰层的冰温及
气温变化。由图 7 可见，冰温变化与气温的波动存在一定的响应关系，但各层冰温随随时间的波动较
气温更为平缓，表层（10 cm）冰温变化与气温变化趋势较为一致，随着冰层深度的增加，冰温波动幅
度逐渐减小，冰温也逐步升高。气温对冰温的影响深度至多可达 30 cm，冰层深度 30 cm 以下的冰温
随时间变化近似一组水平直线。冰温与气温最小值出现于每日 6 时—7 时，冰温比气温大约滞后 1 h，
最大值出现在下午 12 时—16 时，冰温滞后约 2 h。

— 355 —