Page 104 - 水利学报2021年第52卷第3期

日平均气温/℃

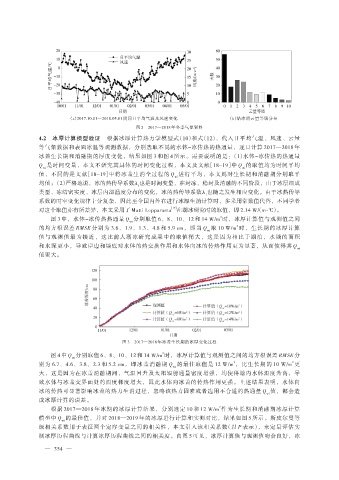
（a）2017.10.01—2018.05.01 期间日平均气温及风速变化 （b）结冰期云量等级分布
图 2 2017—2018 年冬季气象资料
4.2 冰厚计算模型验证 根据冰厚计算热力学模型式（10）和式（12），代入日平均气温、风速、云量

等气象数据和表面冰温等观测数据，分别选取不同的水体-冰传热的热通量，逐日计算 2017—2018 年
冰盖生长期和消融期的厚度变化，结果如图 3 和图 4 所示。需要说明的是：（1）水体-冰传热的热通量
Q 是时间变量，本文不研究其具体的时间变化过程，本文及文献［18-19］中 Q 的取值均为时间平均
wi wi
值，不同的是文献［18-19］中将冰盖生消全过程的 Q 进行平均，本文则对生长期和消融期分别取平
wi
均值；（2）严格地说，冰的热传导系数λ 也是时间变量，在封冻、稳封及消融的不同阶段，由于冰层组成
i
类型、冻结密实度、冰层内部温度分布的变化，冰的热传导系数λ 也随之发生相应变化。由于冰热传导
i
系数的时空变化规律十分复杂，因此至今国内外在进行冰厚生消计算时，多采用常数值代替，不同学者
［17］
对这个取值亦有所差异，本文采用了 Matti Lepparanta 在湖冰研究时的取值，即 2.14 W/（m·℃）。
图 3 中，水体-冰传热热通量 Q 分别取值 6、8、10、12 和 14 W/m 时，冰厚计算值与观测值之间
2
wi
的均方根误差 RMSE 分别为 3.6、1.9、1.3、4.8 和 5.9 cm，即当 Q 取 10 W/m 时，生长期的冰厚计算
2
wi
值与观测值最为接近，这比前人湖冰研究成果中的取值稍大，这是因为相比于湖泊，水塘的面积
和水深更小，导致岸边和塘底对水体的热交换作用和水体向冰的传热作用更为显著，从而使得其 Q
wi
值更大。

图 3 2017—2018 年冰盖生长期的冰厚变化过程
图 4 中 Q 分别取值 6、8、10、12 和 14 W/m 时，冰厚计算值与观测值之间的均方根误差 RMSE 分
2
wi
别为 6.7、4.6、3.8、2.3 和 5.2 cm，即冰盖消融期 Q 的最佳取值是 12 W/m ，比生长期的 10 W/m 更
2
2
wi
大，这是因为在冰盖消融期间，气温回升及太阳辐射通量密度增强，均使得塘内水体温度升高，导
致水体与冰盖交界面处的温度梯度增大，因此水体向冰盖的传热作用更强。上述结果表明，水体向
冰的传热可显著影响冰盖的热力生消过程，忽略该热力因素或者选用不合适的热通量 Q 值，都会造
wi
成冰厚计算的误差。
2
根据 2017—2018 年冰期的冰厚计算结果，分别选定 10 和 12 W/m 作为生长期和消融期冰厚计算
模型中 Q 的最佳值，并对 2018—2019 年的冰厚进行计算和实测对比，结果如图 5 所示。斯皮尔曼等
wi
级相关系数用于表征两个定序变量之间的相关性，本文引入该相关系数（以 P 表示），来定量评估实
测冰厚历程曲线与计算冰厚历程曲线之间的相关度。由图 5 可见，冰厚计算值与观测值吻合良好，冰

— 354 —