Page 37 - 水利学报2021年第52卷第4期

（1）悬移质含沙量 S 与水沙综合参数 C 的关系。在河床处于相对冲淤平衡状态且水流与河床中
各组分泥沙充分交换时，认为选取的悬移质总含沙量 S（不扣除冲泻质部分）即为水流挟沙力，那么
挟沙力级配近似等于悬移质级配，则根据悬移质级配计算得到平均沉速 ω ，进而求得水沙综合参
m
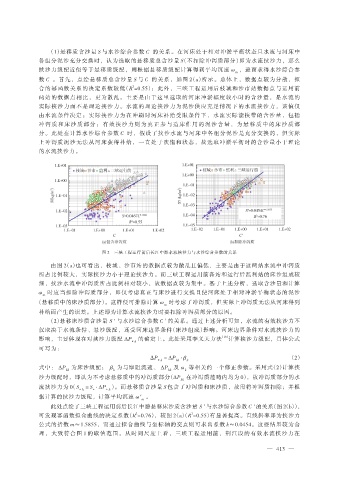
数 C 。首先，点绘悬移质总含沙量 S 与 C 的关系，如图 2（a）所示。总体上，数据点较为分散，拟
2
合的幂函数关系的决定系数较低（R =0.55）；此外，三峡工程运用后枝城和沙市站数据点与运用前
两站的数据点相比，更为散乱。主要是由于这里选取的河床冲淤幅度较小时的含沙量，是水流的
实际挟沙力而不是理论挟沙力。水流的理论挟沙力为泥沙供应充足情况下的水流挟沙力，该值仅
由水流条件决定；实际挟沙力为在冲刷时河床补给受限条件下，水流实际能挟带的含沙量，包括
冲 泻 质 和 床 沙 质 部 分 ； 有 效 挟 沙 力 则 为 真 正 参 与 造 床 作 用 的 泥 沙 含 量 ， 为 悬 移 质 中 的 床 沙 质 部
分。此处在计算水沙综合参数 C 时，假设了挟沙水流与河床中各组分泥沙是充分交换的，但实际
上冲泻质泥沙无法从河床获得补给，一直处于次饱和状态，故选取冲淤平衡时的含沙量小于理论
的水流挟沙力。

图 2 三峡工程运行前后长江中游水流挟沙力与水沙综合参数的关系

由图 2（a）也可看出，枝城、沙市站的数据点较为散乱且偏低，主要是由于这两站水流中冲泻质
所占比例较大，实际挟沙力小于理论挟沙力。而三峡工程运用前各站和运行后监利站的床沙组成较
细，挟沙水流中冲泻质所占比例相对较小，故数据点较为集中。基于上述分析，选取含沙量和计算
ω 时应当扣除冲泻质部分，即仅考虑真正与床沙进行交换且使河床处于相对冲淤平衡状态的泥沙
m
（悬移质中的床沙质部分）。这样便可排除计算 ω 时考虑了冲泻质，但实际上冲泻质无法从河床得到
m
补给而产生的误差。上述即为计算水流挟沙力时要扣除冲泻质部分的原因。
（2）悬移床沙质含沙量 S ′ 与水沙综合参数 C ′ 的关系。通过上述分析可知，水流的有效挟沙力不
仅取决于水流条件、悬沙级配，还受河床边界条件（床沙组成）影响。河床边界条件对水流挟沙力的
影响，主要体现在对挟沙力级配 ΔP ∗k 的确定上。此处采用李义天方法 ［18］ 计算挟沙力级配，具体公式
可写为：
ΔP ∗k = ΔP ⋅ β k （2）
bk
式中： ΔP bk 为床沙级配； β 为与摩阻流速、 ΔP bk 及 ω 等相关的一个修正参数。采用式（2）计算挟
k
k
沙力级配时，即认为不考虑悬移质中的冲泻质部分（ΔP bk 在冲泻质范畴内均为 0），故冲泻质部分的水
流挟沙力为 0（S ∗k = S ⋅ ΔP ）。而悬移质含沙量 S 包含了冲泻质和床沙质，故需将冲泻质扣除；并根
∗k
∗
据计算的挟沙力级配，计算平均沉速 ω ′ 。
m
此处点绘了三峡工程运用前后长江中游悬移床沙质含沙量 S ′ 与水沙综合参数 C ′ 的关系（图 2（b）），
可发现幂函数拟合曲线的决定系数（R =0.76），较图 2（a）（R =0.55）有显著提高。直线斜率即为挟沙力
2
2
公式的指数 m≈1.5855，而通过拟合曲线与坐标轴的交点则可求出系数 k≈0.0454。这些结果较为合
理，大致符合图 1 的取值范围。从时间尺度上看，三峡工程运用前，荆江段的有效水流挟沙力在

— 413 —