Page 40 - 水利学报2021年第52卷第4期

在模型计算中，以枝城站日均的流量、含沙量和悬沙级配资料作为上游边界条件；同时采用莲
花塘站的日均水位过程作为下游边界条件；还需将三口分流的日均流量、含沙量和悬沙级配作为侧
3
向边界条件。2016 年枝城站最小、最大和平均流量分别为 6950、34 000 和 14 000 m /s，且最小、最
3
大和平均含沙量为 0.003、0.147 及 0.016 kg/m ；在莲花塘站，水位在 18.70～32.32 m 之间变化（图 6）。
另外，采用荆江段 173 个汛后实测固定断面地形和 72 个固定断面的实测床沙级配（施测时间为 2015 年
10 月）作为初始河床边界条件，其中床沙的中值粒径范围为 0.17 ~ 0.33 mm；其余断面的初始级配由
［21-22］
这些实测值插值求得。由于在长江中游河段，推移质输沙量仅占悬移质输沙量的 1%～2% ，对河
床变形的影响很小，故在冲淤计算中未考虑推移质输移的影响。

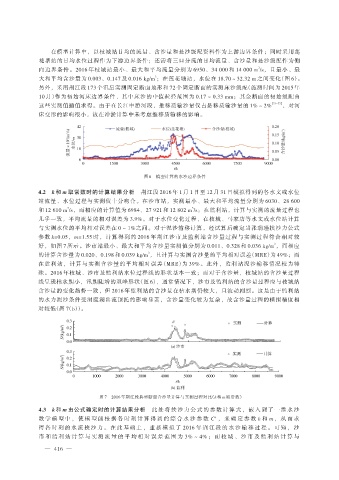
图 6 模型计算的水沙边界条件

4.2 k 和 m 取常数时的计算结果分析 荆江段 2016 年 1 月 1 日至 12 月 31 日模拟得到的各水文或水位

站流量、水位过程与实测值十分吻合。在沙市站，实测最小、最大和平均流量分别为 6030、28 600
3
和 12 610 m /s，而相应的计算值为 6984、27 921 和 12 802 m /s；在监利站，计算与实测的流量过程也
3
几乎一致，平均流量的相对误差为 3.9%。对于水位变化过程，在枝城、马家店等水文或水位站计算
与实测水位的平均相对误差在 0 ~ 1%之间。对于泥沙输移计算，经试算后确定当张瑞瑾挟沙力公式
参数 k=0.05，m=1.55 时，计算得到的 2016 年荆江沙市及监利站含沙量过程与实测过程符合相对较
好，如图 7 所示。沙市站最小、最大和平均含沙量实测值分别为 0.011、0.328 和 0.036 kg/m ，而相应
3
的计算含沙量为 0.020、0.198 和 0.039 kg/m ，且计算与实测含沙量的平均相对误差（MRE）为 49%；而
3
在监利站，计算与实测含沙量的平均相对误差（MRE）为 39%。此外，监利站泥沙输移情况较为特
殊。2016 年枝城、沙市及监利站水位过程线的形状基本一致；而对于含沙量，枝城站的含沙量过程
线呈现枯水期小，汛期陡增的双峰形状（图 6），通常情况下，沙市及监利站的含沙量过程应与枝城站
含沙量的变化趋势一致，但 2016 年监利站的含沙量在枯水期仍较大，且波动剧烈。这是由于监利站
的水力泥沙条件受洞庭湖出流顶托的影响显著，含沙量变化较为复杂，故含沙量过程的模拟精度相
对较低（图 7（b））。

图 7 2016 年荆江段典型断面含沙量计算与实测过程对比（k 和 m 取常数）
4.3 k 和 m 由公式确定时的计算结果分析 此 处 将 挟 沙 力 公 式 的 参 数 计 算 式 ， 嵌 入 到 了 一 维 水 沙
数 学 模 型 中 ， 使 模 型 能 根 据 各 时 刻 计 算 得 到 的 综 合 水 沙 参 数 C' ， 来 确 定 参 数 k 和 m， 从 而 求
得 各 时 刻 的 水 流 挟 沙 力 。 在 此 基 础 上 ， 重 新 模 拟 了 2016 年 荆 江 段 的 水 沙 输 移 过 程 。 可 知 ， 沙
市 和 监 利 站 计 算 与 实 测 流 量 的 平 均 相 对 误 差 范 围 为 3% ~ 4% ； 而 枝 城 、 沙 市 及 监 利 站 计 算 与

— 416 —