Page 70 - 水利学报2021年第52卷第5期

400 400 400

300 300 300
y/cm 200 y/cm 200 y/cm 200

100 100 100

0 0 0
0 100 200 300 400 0 100 200 300 400 0 100 200 300 400
x/cm x/cm x/cm
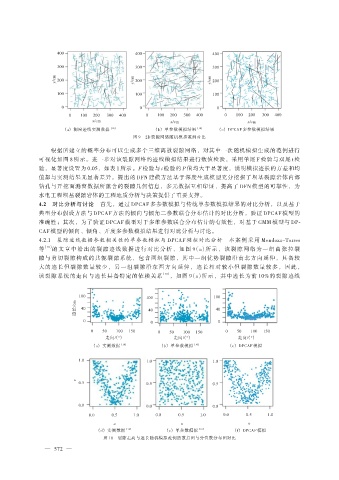
（a） 测窗迹线实测数据 ［10］ （b） 单参数模拟结果 ［10］ （c） DPCAF 多参数模拟结果
图 9 2D 裂隙网络随机模拟范例对比
根据所建立的概率分布可以生成多个三维离散裂隙网络，对其中一次随机模拟生成的范例进行
可视化如图 8 所示。进一步对该裂隙网络的迹线模拟结果进行数值检验，采用单尾 F 检验与双尾 t 检
验，显著度设置为 0.05，如表 1 所示。F 检验与 t 检验的 P 值均大于显著度，说明模拟迹长的方差和均
值都与实测结果无显著差异。提出的 DFN 建模方法基于深度生成模型充分挖掘了坝基裂隙岩体内部
钻孔与开挖面测窗数据所蕴含的裂隙几何信息，多元数据互相印证，提高了 DFN 模型的可靠性，为
水电工程坝基裂隙岩体的工程地质分析与决策提供了重要支撑。
4.2 对比分析与讨论 首先，通过 DPCAF 多参数模拟与传统单参数模拟结果的对比分析，以及基于
典型分布假设方法与 DPCAF 方法的倾向与倾角二参数联合分布估计的对比分析，验证 DPCAF 模型的
准确性；其次，为了验证 DPCAF 模型对于多维参数联合分布估计的有效性，对基于 GMM 模型与 DP⁃
CAF 模型的倾向、倾角、开度多参数模拟结果进行对比分析与讨论。
4.2.1 裂隙迹线数据参数相关性的单参数模拟与 DPCAF 模拟对比分析 本案例采用 Mendoza-Torres
等 ［10］ 的 文 章 中 给 出 的 裂 隙 迹 线 数 据 进 行 对 比 分 析 ， 如 图 9（a）所 示 ， 该 裂 隙 网 络 为 一 组 由 张 拉 裂
隙与剪切裂隙构成的共轭裂隙系统，包含两组裂隙，其中一组优势裂隙沿南北方向延伸，具备较
大的迹长但裂隙数量较少，另一组裂隙沿东西方向延伸，迹长相对较小但裂隙数量较多，因此，
该裂隙系统的走向与迹长具备特定的依赖关系 ［10］ ，如图 9（a）所示，其中迹长为前 10%的裂隙迹线

100 100 100
迹长/cm 40 40 40

0 0
0
0 50 100 150 0 50 100 150 0 50 100 150
走向/（°） 走向/（°） 走向/（°）
（a） 实测数据 ［10］ （b） 单参数模拟 ［10］ （c） DPCAF 模拟

1.0 1.0 1.0

v
0.5 0.5 0.5

0.0 0.0 0.0
0.0 0.5 1.0 0.0 0.5 1.0 0.0 0.5 1.0
u u u
（d） 实测数据 ［10］ （e） 单参数模拟 ［10］ （f） DPCAF 模拟
图 10 裂隙走向与迹长随机模拟范例的散点图与分位数分布图对比
— 572 —