Page 67 - 水利学报2021年第52卷第5期

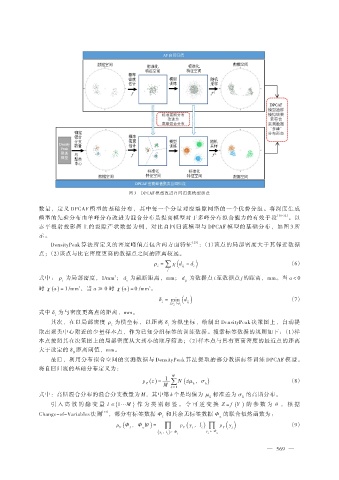
图 3 DPCAF 模型改进自回归流模型示意

数量，定义 DPCAF 模型的基础分布，其中每一个分量对应裂隙网络的一个优势分组。将深度生成
模型的先验分布由单峰分布改进为混合分布是提高模型对于多峰分布拟合能力的有效手段 ［30-32］ 。以
赤平极射投影图上的裂隙产状数据为例，对比自回归流模型与 DPCAF 模型的基础分布，如图 3 所
示。
DensityPeak 算法所定义的密度峰值点包含两方面特征 ［25］ ：（1）该点的局部密度大于其邻近数据
点；（2）该点与比它密度更高的数据点之间的距离较远。
ρ = χ ij c ) （6）
i å ( d - d
j
3
式中： ρ 为局部密度，1/mm ； d 为截断距离，mm； d 为数据点 i 至数据点 j 的距离，mm。当 a < 0
i
c
ij
a
a
时 χ ( ) = 1 /mm ，当 a ≥ 0 时 χ ( ) = 0 /mm 。
3
3
δ = min ( ) （7）
d
i
j:ρ > ρ
j i ij
式中 δ 为与密度更高点的距离，mm。
i
其次，在以局部密度 ρ 为横坐标，以距离 δ 为纵坐标，绘制出 DensityPeak 决策图上，自动提
i
i
取出聚类中心附近的少量样本点，作为已知分组标签的训练数据。搜索标签数据的规则如下：（1）样
本点按照其在决策图上的局部密度从大到小的顺序筛选；（2）样本点与具有更高密度的最近点的距离
大于设定的 δ 距离阈值，mm。
0
最后，利用分布拟合空间的实测数据与 DensityPeak 算法提取的部分数据标签训练 DPCAF 模型。
将自回归流的基础分布定义为：
M
p ( ) z = 1 å ( z|μ ，σ k ) （8）
N
k
M
Z
k = 1
式中：高斯混合分布的混合分支数量为 M，其中第 k 个是均值为 μ 标准差为 σ 的高斯分布。
k
k
引 入 离 散 的 隐 变 量 l ∈{1M } 作 为 类 别 标 签 。 令 可 逆 变 换 Z = f ( ) 的 参 数 为 θ ， 根 据
Y
Change-of-Variables 法则 ［14］ ，部分有标签数据 Φ 和其余无标签数据 Φ 的联合似然函数为：
l
u
)
p (Φ ，Φ |θ = Õ p ( y ，l i ) Õ p ( ) （9）
y
j
Y
i
l
u
Y
Y
)
( y ，l ∈ Φ l y ∈ Φ u
j
i
i
— 569 —