Page 65 - 2021年第52卷第8期

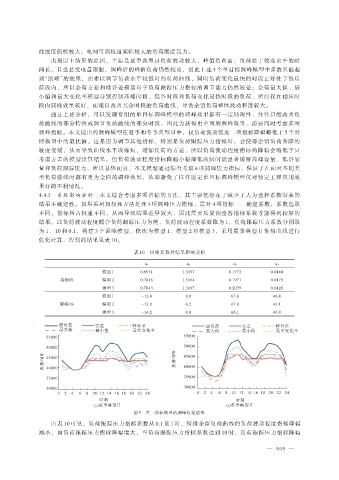
线坡度仍然较大，电网可调机组面临较大的负荷跟踪压力。
出现以上结果的原因，主要是夏季典型日负荷波动较大，峰值负荷高，负荷处于较高水平的时
间长，且受总发电量限制，调峰后的峰值负荷仍然较高，因此上述 5 个单目标调峰模型中多数只能起
到“削峰”的效果，而难以调节负荷水平较低时的负荷曲线，同时负荷变化最快的时段正好处于低负
荷段内，所以余荷方差和峰谷差模型对于负荷跟踪压力指标的调节能力仍然较差；余荷最大值、最
小值和最大变化率模型分别控制高峰时段、低谷时段和负荷变化最快时段的负荷，所以仅在相应时
段内调峰效果较好，而难以改善其余时段的负荷曲线，导致余留负荷整体波动程度较大。
通过上述分析，可以发现常用的单目标调峰模型的调峰效果都有一定局限性，往往只能改善负
荷曲线的部分特性或调节负荷曲线的部分时段，因此为获得更全面的调峰效果，需要同时考虑多项
调峰指标。本文提出的调峰模型在夏季和冬季典型日中，仅负荷波动程度一项指标降幅略低于 5 个对
照模型中的最优值。这是因为调节其他指标，特别是负荷跟踪压力指标时，会使得余留负荷升降的
坡度变缓，从而导致曲线水平段缩短，增加负荷的方差，所以负荷波动程度指标的降幅会略低于只
考虑方差的模型计算结果。但负荷波动程度指标降幅小幅降低的同时能显著缓解高峰容量、低谷容
量和负荷跟踪压力，所以总体而言，本文模型通过综合考虑 4 项调峰压力指标，保证了在面对不同类
型负荷曲线时都有更为全面的调峰效果，从而避免了以往固定单目标调峰模型仅对特定工程应用效
果好的不利情况。
4.4.3 系数影响分析 本文综合考虑多项指标的方法，其主要优势在于减少了人为选择系数带来的
结果不确定性。如果采用加权和方法处理 4 项调峰压力指标，需对 4 项指标一一确定系数，系数选取
不同，指标所占权重不同，从而导致结果差异较大，因此需要反复调整各指标系数才能得到较好的
结果。以负荷波动程度耦合负荷跟踪压力为例，负荷波动程度系数取为 1，负荷跟踪压力系数分别取
为 1、10 和 0.1，构建 3 个调峰模型，依次为模型 1、模型 2 和模型 3，采用夏季典型日负荷曲线进行
优化计算，得到的结果见表 10。

表 10 权重系数对结果影响分析

α 1 α 2 α 3 α 4
模型 1 0.6931 1.3197 0.1972 0.0444
指标值 模型 2 0.7018 1.3164 0.1971 0.0475
模型 3 0.7043 1.3197 0.2079 0.0426
模型 1 -12.4 0.0 67.8 46.8
降幅/% 模型 2 -13.8 0.2 67.8 43.1
模型 3 -14.2 0.0 66.1 49.0

原负荷 方差 峰谷差 原负荷 方差 峰谷差
最大值 最小值 最大变化率 最大值 最小值 最大变化率
55000 55000
50000 50000
负荷/MW 45000 负荷/MW 45000

40000
40000
35000 35000
30000 30000
0 2 4 6 8 10 12 14 16 18 20 22 24 0 2 4 6 8 10 12 14 16 18 20 22 24
时刻 时刻
(a)夏季典型日 (a)冬季典型日
图 5 单一指标模型的调峰优化结果
由表 10 可见，负荷跟踪压力指标系数从 0.1 至 1 时，所得余留负荷曲线的负荷波动程度指标降幅
减小，而负荷跟踪压力指标降幅增大，当负荷跟踪压力指标系数达到 10 时，负荷跟踪压力指标降幅

— 945 —