Page 64 - 2021年第52卷第8期

致；负荷波动程度分别减少了 45.0%和 34.0%，余留负荷曲线整体更为平滑。由此可见，本文提出的
调峰模型在不同条件下均有较好的调峰效果。
4.4.2 调峰效果对比分析 为说明本文模型与单目标调峰模型的调峰效果差异，分别与常用的 5 个单
目标调峰模型进行比较，目标函数分别为余荷方差、峰谷差、最大值、最小值和最大变化率，计算
结果见表 8、表 9。

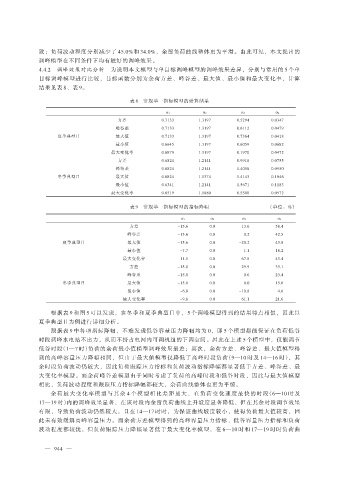
表 8 常规单一指标模型的计算结果

α 1 α 2 α 3 α 4
方差 0.7133 1.3197 0.5294 0.0347
峰谷差 0.7133 1.3197 0.6112 0.0479
夏季典型日 最大值 0.7133 1.3197 0.7364 0.0418
最小值 0.6645 1.3197 0.6059 0.0682
最大变化率 0.6879 1.3197 0.1970 0.0472
方差 0.6824 1.2141 0.9918 0.0755
峰谷差 0.6824 1.2141 1.4058 0.0950
冬季典型日 最大值 0.6824 1.1374 1.4143 0.1046
最小值 0.6341 1.2141 1.5671 0.1183
最大变化率 0.6519 1.1880 0.5500 0.0972

表 9 常规单一指标模型的指标降幅 （单位：%）

α 1 α 2 α 3 α 4
方差 -15.6 0.0 13.6 58.4
峰谷差 -15.6 0.0 0.2 42.5
夏季典型日 最大值 -15.6 0.0 -20.2 49.8
最小值 -7.7 0.0 1.1 18.2
最大变化率 -11.5 0.0 67.8 43.4
方差 -15.0 0.0 29.9 39.1
峰谷差 -15.0 0.0 0.6 23.4
冬季典型日 最大值 -15.0 0.0 0.0 15.6
最小值 -6.8 0.0 -10.8 4.6
最大变化率 -9.8 0.0 61.1 21.6

根据表 9 和图 5 可以发现，在冬季和夏季典型日中，5 个调峰模型得到的结果特点相似，因此以
夏季典型日为例进行详细分析。
跟据表 9 中各项指标降幅，不难发现低谷容量压力降幅均为 0，即 5 个模型都能保证在负荷低谷
时段调峰水电站不出力，从而不挤占电网内可调机组的下调空间。因此在上述 5 个模型中，仅能调节
低谷时段（1—7 时）负荷的余荷最小值模型调峰效果最差；其次，余荷方差、峰谷差、最大值模型得
到的高峰容量压力降幅相同，但由于最大值模型仅降低了高峰时段负荷（9—10 时及 14—16 时），其
余时段负荷波动仍较大，因此负荷跟踪压力指标和负荷波动指标降幅都显著低于方差、峰谷差、最
大变化率模型。而余荷峰谷差模型由于同时考虑了负荷的高峰时段和低谷时段，因此与最大值模型
相比，负荷波动程度和跟踪压力指标降幅都较大，余荷曲线整体也更为平缓。
余荷最大变化率模型与其余 4 个模型相比差距最大，在负荷变化速度最快的时段（6—10 时及
17—19 时）内的调峰效果显著，在该时段内余留负荷曲线上升坡度显著降低，但在其余时段调节效果
有限，导致负荷波动仍然较大，且在 14—17 时时，为保证曲线坡度较小，使得负荷最大值较高，因
此未有效缓解高峰容量压力。而余荷方差模型得到的高峰容量压力指标、低谷容量压力指标和负荷
波动程度都较优，但负荷跟踪压力降幅显著低于最大变化率模型，在 6—10 时和 17—19 时时负荷曲

— 944 —