Page 40 - 水利学报2021年第52卷第11期

振次 N（次） 振次 N（次）
（a） （b）

振次 N（次） 振次 N（次）
（c） （d）
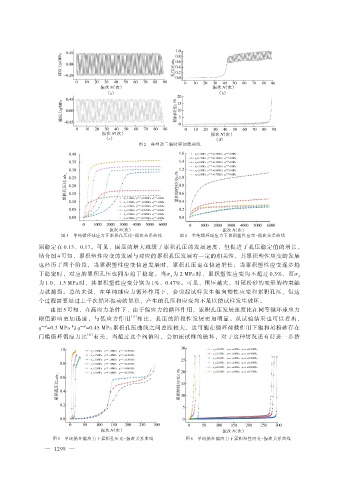
图 2 典型动三轴时程加载曲线

振次 N（次） 振次 N（次）
图 3 单纯循环球应力下累积孔压比-振次关系曲线 图 4 单纯循环球应力下累积塑性应变-振次关系曲线

别稳定在 0.13、0.17。可见，围压的增大减缓了累积孔压的发展速度，但促进了孔压稳定值的增长。
结合图 4 可知，累积塑性应变的发展与对应的累积孔压发展有一定的相关性，其累积塑性应变的发展
也经历了两个阶段，当累积塑性应变快速发展时，累积孔压也在快速增长；当累积塑性应变逐步趋
于稳定时，对应的累积孔压也同步趋于稳定。当σ 为 2 MPa 时，累积塑性应变均不超过 0.3%，而σ
3 3
为 1.0、1.5 MPa 时，其累积塑性应变分别为 1%、0.47%。可见，围压越大，对尾粉砂的变形的约束能
力就越强。总的来说，在单纯球应力循环作用下，会引起试样发生轴向塑性应变和累积孔压，但这
个过程需要经过上千次循环振动的累积，产生的孔压和应变均不足以使试样发生破坏。
由图 5 可知，在高应力条件下，由于偏应力的循环作用，累积孔压发展速度比在同等循环球应力
幅值影响更加迅速，与低应力作用 ［17］ 相比，孔压的阶段性发展更加明显。从试验结果也可以看出，
q ampl =0.3 MPa 与 q ampl =0.45 MPa 累积孔压曲线之间差距较大，这可能在循环荷载作用下饱和尾粉砂存在
门槛循环偏应力比 ［21］ 有关，当超过这个阀值时，会加速试样的破坏，对于这种情况还有待进一步撰

振次 N（次） 振次 N（次）
图 5 单纯循环偏应力下累积孔压比-振次关系曲线 图 6 单纯循环偏应力下累积塑性应变-振次关系曲线
— 1298 —