Page 43 - 水利学报2021年第52卷第11期
P. 43
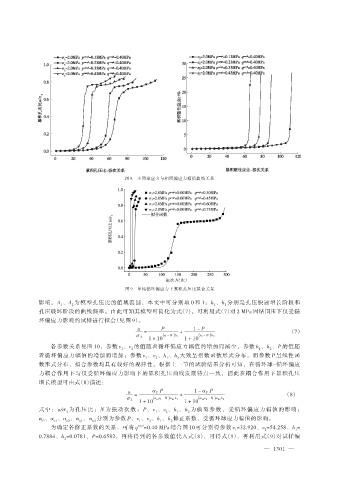
图 8 不同球应力与相同偏应力幅值曲线关系
振次 N(次)
图 9 单纯循环偏应力下累积孔压比拟合关系
影响。A 、A 为模型孔压比的值域范围,本文中可分别取 0 和 1;h 、h 分别是孔压快速增长阶段和
1 2 1 2
孔压破坏阶段的曲线斜率。由此可知其模型可简化为式(7)。可利用式(7)对 2 MPa 固结围压下仅受循
环偏应力影响的试样进行拟合(见图 9)。
u = P + 1 - P (7)
σ 3 (v 1 - N )h 1 (v 2 - N )h 2
1 + 10 1 + 10
各参数关系见图 10,参数 v 、v 的值随着循环偏应力幅值的增加而减少,参数 h 、h 、P 的值随
1 2 1 2
着循环偏应力幅值的增加而增加;参数 v 、v 、h 、h 大致呈指数函数形式分布,而参数 P 呈线性函
1 2 1 2
数形式分布,拟合参数均具有较好的规律性。根据上一节的试验结果分析可知,在循环球-循环偏应
力耦合作用下与仅受循环偏应力影响下的累积孔压曲线发展特点一致,因此在耦合作用下累积孔压
增长模型可由式(8)描述:
u = α P P + 1 - α P P (8)
(α v1 v 1 - N (α v2 v 2 - N
σ 3 )α h1 h 1 )α h2 h 2
1 + 10 1 + 10
式中:u/σ 为孔压比;N 为振动次数;P、v 、v 、h 、h 为模型参数,受循环偏应力幅值的影响;
3 1 2 1 2
α 、α 、α 、α 、α 分别为参数 P、v 、v 、h 、h 修正系数,受循环球应力幅值的影响。
P
2
1
2
1
v2
v1
h2
h1
为确定各修正系数的关系,可将 q ampl =0.40 MPa 结合图 10 可分别得参数 v =32.920、v =54.258、h =
1 2 1
0.7884、h =0.0781、P=0.6582,再将得到的各参数值代入式(8),可得式(9),再利用式(9)对试样编
2
— 1301 —