Page 110 - 2022年第53卷第1期

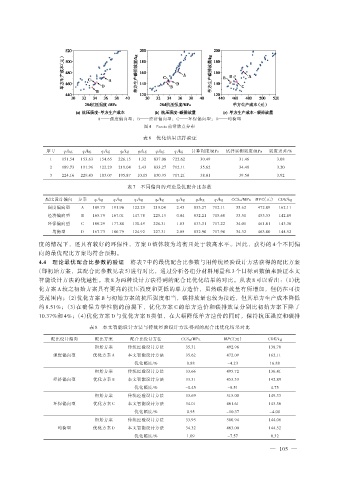
A——强度偏向型；B——经济偏向型；C——环保偏向型；D——均衡型
图 4 Pareto 前沿散点分布
表 6 优化结果试拌验证

序号 q 1/kg q 2/kg q 3/kg q 4/kg q 5/kg q 6/kg q 7/kg 计算强度/MPa 试拌实测强度/MPa 强度误差/%
1 151.54 153.63 154.65 226.15 1.32 837.08 722.62 30.49 31.46 3.08
2 189.73 191.96 122.29 219.04 2.43 833.27 712.11 35.62 34.48 3.20
3 224.16 229.43 103.07 195.87 10.15 830.95 717.21 38.01 39.50 3.92

表 7 不同偏向的理论最优配合比参数
配比设计偏向 方案 q 1/kg q 2/kg q 3/kg q 4/kg q 5/kg q 6/kg q 7/kg CCS 28/MPa MPC（元） CDE/kg
强度偏向型 A 189.73 191.96 122.29 219.04 2.43 833.27 712.11 35.62 472.09 162.11
经济偏向型 B 165.79 167.01 147.78 225.13 0.04 832.21 715.60 33.51 453.53 142.89
环保偏向型 C 166.29 177.88 130.49 226.31 1.83 833.31 717.22 34.01 461.61 143.36
均衡型 D 167.73 180.79 124.92 227.31 2.05 832.90 717.90 34.32 463.00 144.52

度的情况下，还具有较好的环保性，方案 D 整体较为均衡且处于较高水平。因此，获得的 4 个不同偏
向的最优配比方案均符合预期。
4.4 理论最优配合比参数的验证 将表 7 中的最优配合比参数与用传统经验设计方法获得的配比方案

（即初始方案，其配合比参数见表 5）进行对比，通过分析各组分材料用量和 3 个目标函数值来验证本文
智能设计方法的优越性。表 8 为两种设计方法得到的配合比优化结果的对比。从表 8 可以看出：（1）优
化方案 A 较之初始方案具有更高的抗压强度和更低的单方造价，虽然碳排放量有所增加，但仍在可接
受范围内；（2）优化方案 B 与初始方案的抗压强度相当，碳排放量也较为接近，但其单方生产成本降低
约 8.51%；（3）在确保力学性能的前提下，优化方案 C 的单方造价和碳排放量分别比初始方案下降了
10.37%和 4%；（4）优化方案 D 与优化方案 B 类似，在大幅降低单方造价的同时，保持抗压强度和碳排

表 8 本文智能设计方法与传统经验设计方法得到的配合比优化结果对比
配比设计偏向 配比方案 配合比设计方法 CCS 28/MPa MPC（元） CDE/kg
初始方案 传统经验设计方法 35.31 492.96 138.70
强度偏向型 优化方案 A 本文智能设计方法 35.62 472.09 162.11
优化幅度/% 0.88 -4.23 16.88
初始方案 传统经验设计方法 33.66 495.72 136.41
经济偏向型 优化方案 B 本文智能设计方法 33.51 453.53 142.89
优化幅度/% -0.45 -8.51 4.75
初始方案 传统经验设计方法 33.69 515.00 149.33
环保偏向型 优化方案 C 本文智能设计方法 34.01 461.61 143.36
优化幅度/% 0.95 -10.37 -4.00
初始方案 传统经验设计方法 33.95 500.94 144.06
均衡型 优化方案 D 本文智能设计方法 34.32 463.00 144.52
优化幅度/% 1.09 -7.57 0.32

— 105 —