Page 109 - 2022年第53卷第1期

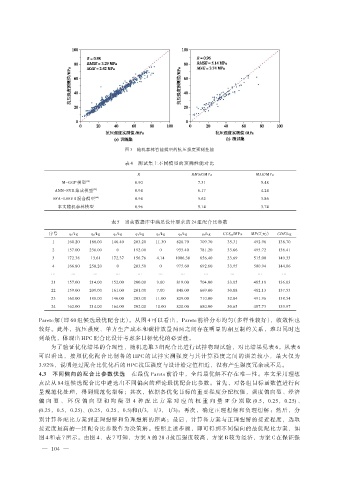
图 3 随机森林智能模型的抗压强度预测性能

表 4 测试集上不同模型的预测性能对比
R RMSE/MPa MAE/MPa
M-GGP 模型 [38] 0.90 7.31 5.48
ANN-SVR 集成模型 [39] 0.94 6.17 4.24
SFA-LSSVR 混合模型 [40] 0.94 5.62 3.86
本文随机森林模型 0.96 5.14 3.74

表 5 当前数据库中满足设计要求的 24 组配合比参数

序号 q 1/kg q 2/kg q 3/kg q 4/kg q 5/kg q 6/kg q 7/kg CCS 28/MPa MPC（元） CDE/kg
1 160.20 188.00 146.40 203.20 11.30 828.70 709.70 35.31 492.96 138.70
2 157.00 236.00 0 192.00 0 935.40 781.20 33.66 495.72 136.41
3 172.38 13.61 172.37 156.76 4.14 1006.30 856.40 33.69 515.00 149.33
4 166.80 250.20 0 203.50 0 975.60 692.60 33.95 500.94 144.06
… … … … … … … … … … …
21 157.00 214.00 152.00 200.00 9.00 819.00 704.00 33.05 485.18 136.03
22 159.00 209.00 161.00 201.00 7.00 848.00 669.00 30.88 482.13 137.53
23 160.00 188.00 146.00 203.00 11.00 829.00 710.00 32.84 491.96 138.54
24 162.00 214.00 164.00 202.00 10.00 820.00 680.00 30.65 487.73 139.97

Pareto 解（即 60 组候选最优配合比）。从图 4 可以看出，Pareto 前沿分布均匀（多样性较好），收敛性也
较好。此外，抗压强度、单方生产成本和碳排放量两两之间存在明显的相互制约关系，难以同时达
到最优，体现出 HPC 配合比设计考虑多目标优化的必要性。
为了验证优化结果的合理性，随机选取 3 组配合比进行试拌物理试验，对比结果见表 6。从表 6
可以看出，按照优化配合比制备的 HPC 的试拌实测强度与其计算强度之间的误差较小，最大仅为
3.92%，说明经过配合比优化后的 HPC 抗压强度与设计给定值相近，没有产生强度冗余或不足。
4.3 不同偏向的配合比参数优选 在最优 Pareto 前沿中，全局最优解不存在唯一性。本文采用理想
点法从 84 组候选配合比中遴选出不同偏向的理论最优配合比参数。首先，对各组目标函数值进行向
量规范化处理，得到规范化指标；其次，依据各优化目标的重要程度分配权值，强度偏向型、经济
偏 向 型 、 环 保 偏 向 型 和 均 衡 型 4 种 配 比 方 案 对 应 的 权 重 向 量 W 分 别 取 (0.5，0.25，0.25) 、
(0.25，0.5，0.25)、(0.25，0.25，0.5)和(1 3， 1 3， 1 3)；再次，确定正理想解和负理想解；然后，分
别计算各配比方案到正理想解和负理想解的距离；最后，计算各方案与正理想解的接近程度，选取
接近度最高的一组配合比参数作为决策解。按照上述步骤，即可得到不同偏向的最优配比方案，如
图 4 和表 7 所示。由图 4、表 7 可知，方案 A 的 28 d 抗压强度较高，方案 B 较为经济，方案 C 在保证强

— 104 —