Page 107 - 2022年第53卷第1期
P. 107
①初始化种群中各个粒子的位置和速度,并设置初始种群 P,群体规模 N,迭代次数 I 和最大允
许速度 V 。
max
②评价当前种群 P 中所有粒子的各目标值(即适应度值)。
③按照动态加权和非支配排序的策略更新种群 P中各个粒子的个体最优位置 p 和全局最优位置 p 。
g
i
④通过引入自适应惯性权重和变异操作,计算各粒子新的位置和速度,并重新计算每个粒子的
各目标值。
⑤以所得粒子是否接近全局最优解作为收敛准则,若未达到收敛,则返回步骤②,继续更新种
群;若收敛,则输出种群 P 作为 Pareto 解集。
(5)步骤 5。将{ } m 和{ } n 合并为{ } m + n ,根据各优化目标的重要性确定权重向量 W,采用理
Q
Q
Q
2
1
i
i = 1 i i = 1 i i = 1
Q
想点法 [37] 对{ } m + n 中的配比方案进行比选,以获得不同偏向(性能型、经济型、环保型和均衡型)的
i
i = 1
*
理论最优配合比Q 。
*
(6)步骤 6。结合现行规范和设计要求,对上述设计出的理论最优配合比Q 进行试拌、调整,最
**
终得到实际使用的最优配合比Q 。
**
(7)步骤 7。将Q 的试验结果添加到当前数据库中,丰富配合比试验数据,以实现知识的不断累积。
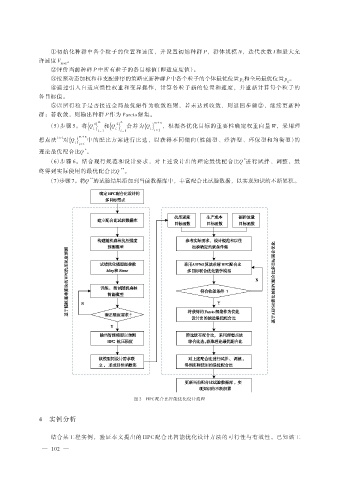
图 2 HPC 配合比智能优化设计流程
4 实例分析
结合某工程实例,验证本文提出的 HPC 配合比智能优化设计方法的可行性与有效性。已知该工
— 102 —