Page 128 - 2022年第53卷第1期

表 1 x=65m 处地下水位动态监测数据（2009.7.11—2009.7.12）与整理
t/h h（x，t）m φ（x，t）×10 /（m·h ） ∂φ（x，t）∂t×10 /（m·h ）
-2
-4
-2
-1
/
/
6 27.617 1.901 0.00
12 27.728 1.853 -0.804
18 27.834 1.769 -1.399
19 27.852 1.754 -1.499
20 27.869 1.739 -1.503
21 27.887 1.724 -1.500
27 27.985 1.637 -1.456
33 28.078 1.557 -1.333
39 28.167 1.485 -1.194
45 28.253 1.421 -1.064
备注 初始潜水位为 27.503m，附近地面高程 30.66m

28.4
-0.1
（m · h -2 ） -0.4 t g=19.5h ∂φ/∂t 28.2 （x，t）m /

28.0
-0.7
∂φ/∂t×10 -4 / -1.0 h（x，t） 27.8 潜水位 h

27.6
-1.3
-1.6 27.4
6 18 30 42
t/h
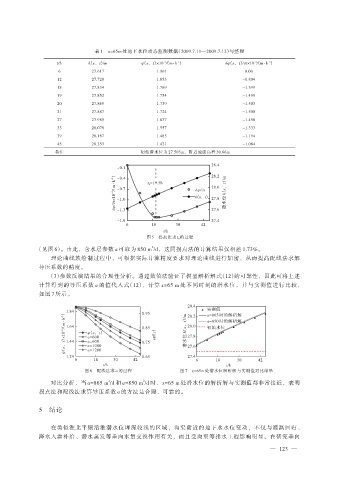
图 5 拐点法求 t g的过程
2
（见图 6）。由此，含水层参数 a 可取为 850 m /d，这同拐点法的计算结果仅相差 1.73%。
理论曲线族绘制过程中，可根据实际计算精度要求对理论曲线进行加密，从而提高配线法求解
导压系数的精度。
（3）参数反演结果的合理性分析。通过数值法验证了模型解析解式（12）的可靠性，因此可将上述
计算得到的导压系数 a 的值代入式（12），计算 x=65 m 处不同时刻的潜水位，并与实测值进行比较，
如图 7 所示。

28.4
实测值
1.84 0.95 28.2 a=865 时的解析解
（m · h -1 ） 1.64 （x，t）m / 28.0 a=850 时的解析解
初始水位
×10 -2 / φ（x，t） 0.85 （z） erf 潜水位 h 27.8
a=600
（x，t） 1.44 a=600 0.75 27.6
a=1000
a=1200
φ
1.24 0.65 27.4
6 18 30 42 6 18 30 42
t/h t/h
图 6 配线法求 a 的过程 图 7 x=65m 处潜水位解析解与实测值对比结果
对比分析，当 a=865 m /d 和 a=850 m /d 时，x=65 m 处潜水位的解析解与实测值都非常接近，表明
2
2
拐点法和配线法求算导压系数 a 的方法是合理、可靠的。

5 结论

在类似淮北平原沿淮潜水位埋深较浅的区域，沟渠附近的地下水水位变动，不仅与灌溉回归、
降水入渗补给、潜水蒸发等垂向水量交换作用有关，而且受沟渠等排水工程影响明显。在研究垂向

— 123 —