Page 125 - 2022年第53卷第1期

的可靠性，通过上述研究中 MacCormack 格式的有限差分法计算相应非线性方程式（1）的数值解，并
将解析解与数值解进行比较。假设 n 时刻各节点的水位 h k，n 均已知，利用 MacCormack 格式的预测校
正两步法进行时间推进，求解出 n+1 时刻各个节点的水位 h 。首先，在预测中对空间导数进行向
k，n+1
前差分，得到用正向差分代替时空导数得到 h 的预测方案 ［21-23］ ，如下：
ε ( ) t k Δt
h ∗ = h + Δt + × [ h k + 1，n (h - h ) - h k，n (h - h ] ) （13）
k，n + 1 k，n μ μ (Δx ) 2 k + 1，n k，n k，n k - 1，n

第二步，对 x 的偏导数用后向差分近似代替，而对于 t 的偏导数用正向差分近似代替，方程式（1）
可写为 ［21-23］ ：
ε ( ) t k Δt
h ∗∗ = h + Δt + 2 [ k，n + 1( h ∗ - h ∗ ) - h ∗ k - 1，n + 1( h ∗ - h ∗ ] ) （14）
× h
∗
k，n + 1 k，n μ μ (Δx ) k + 1，n + 1 k，n + 1 k，n + 1 k - 1，n + 1
最终，h 的修正值为h * 和h ∗∗ 的算术平均值 ［21-23］ ：
k，n+1 k，n + 1 k，n + 1
ì ε ( ) t
h = 1 ï í h + h ∗ + Δt + k Δt ×
k，n + 1 k，n k，n + 1 μ μ 2
2 ï (Δx ) （15）
î
k - 1，n + 1( h
h
[ k，n + 1( h ∗ - h ∗ ) - h ∗ ∗ k，n + 1 - h ∗ } ] )
∗
k + 1，n + 1
k，n + 1
k - 1，n + 1
上述式（13）—（15）构成了非线性方程式（1）的 MacCormack 格式的有限差分法计算方案，其稳定
准则为 ［21-23］ ：
h Δt aΔt
m
μ ) 2 = (Δx ) 2 ≤ 0.5 （16）
k (Δx
根据式（12）—（16），参考淮北平原区域的水文地质特征，模型选取粗砂、中砂、细砂三种含水
［30］ ［30］
层介质，给水度分别设为 0.30、0.22 和 0.17 ，渗透系数分别设为 30 m/d、20 m/d 和 7 m/d ，初始潜
水位取 27.000 m，潜水含水层平均厚度取 3.5 m。计算期为 5 天，假设：第一天、第二天为降水入渗
阶段，对应的降水入渗补给强度分别设为 0.050 m/d 和 0.030 m/d；后三天为潜水蒸发阶段，潜水蒸发强
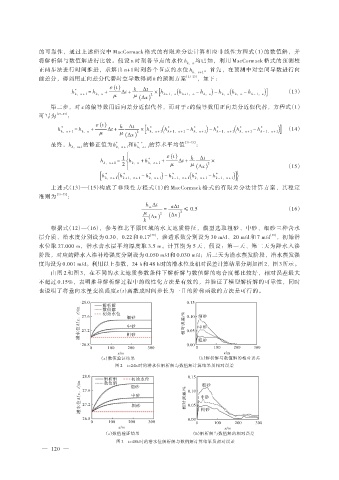
度均设为 0.001 m/d。利用以上参数，24 h和 48 h时的潜水位及相对误差计算结果分别如图 2、图 3所示。
由图 2 和图 3，在不同的水文地质参数条件下解析解与数值解的吻合度都比较好，相对误差最大
不超过 0.15%，表明推导解析解过程中的线性化方法是有效的，并验证了模型解析解的可靠性，同时
也说明了将垂向水量交换强度ε（t）离散成时间步长为一日的阶梯函数的方法是可行的。

28.0 0.15
解析解
（x，t）m 27.6 初始水位 细砂 相对误差/% 0.10 细砂
数值解
/
潜水位 h 27.2 中砂 0.05 中砂
粗砂
26.8 0.00 粗砂
0 100 200 300 0 100 200 300
x/m x/m
（a）数值验证结果 （b）解析解与数值解的相对误差
图 2 t=24h 时的潜水位解析解与数值解计算结果及相对误差
28.0 0.15
解析解 初始水位
（x，t）m / 27.6 细砂 0.10 中砂
数值解
细砂
中砂
潜水位 h 27.2 粗砂 相对误差/% 0.05 粗砂

26.8 0.00
0 100 200 300 0 100 200 300
x/m x/m
（a）数值验证结果 （b）解析解与数值解的相对误差
图 3 t=48h 时的潜水位解析解与数值解计算结果及相对误差
— 120 —