Page 34 - 2022年第53卷第2期

2.1 最佳统计模型优选基本原则 如何在统计模型因子可选域中选出合理的因子组建成最佳统计模

型是解决问题的关键，这与模型优选的原则（决策量）关系密切。综合有关文献关于模型优选的原
则 ［19-20］ ，拟选择拟合的良好性、模型的简单性和检验的有效性为最佳统计模型优选原则。
（1）拟合的良好性：在备选统计模型集合中选出的最佳统计模型必然要求与实测值具有良好的拟
合精度，即最佳统计模型回归分析的复相关系数必须越大越好，反之越差。
（2）模型的简单性：又称最小自由度原则，即优选出的最佳统计模型，不仅要求能较好地描述大
坝工程系统的工作性态，而且还应具有统计模型的因子数较少，以简化计算。即统计模型的因子数
越少越优，反之越差。
（3）检验的有效性：优选得到的最佳统计模型除了拟合效果良好外，还必须满足对大坝工程系统
检验数据系列的预测精度（均方根误差或复相关系数等）能被工程界接受，即是预测实际大坝工程问
题的实用有效模型。
2.2 最佳统计模型优选原则标准化 为了进行统计模型优选，需要将上述 3 个模型优选原则进行无
量纲化及标准化。由于复相关系数、模型因子数和均方根误差不属于同一量级，因此在对回归拟
合、模型因子数和检验效果标准化前，首先需要进行归一化处理。对于拟合的良好性原则，采用式
（1）对复相关系数进行归一化处理；对于模型的简单性和检验的有效性原则，采用式（2）对模型因子
数与均方根误差进行归一化处理。
x - x
x = x - x （1）
min
i
max min
x - x
x = x max - x （2）
j
max min
式中：x 为复相关系数归一化后的无量纲数值；x 为模型因子数和均方根误差归一化后的无量纲数
i
j
值；x 、x 分别为复相关系数、模型因子数和均方根误差的最大值和最小值。
max min
归一化处理后需对回归拟合、模型因子数和检验效果进行标准化，本文采用的标准化公式为：
y = 10( 0.5 - x ) （3）
1
m
1 + e m
式中： y m 为回归拟合、模型因子数和检验效果进行标准化后的无量纲数值；x 为回归拟合、模型因
m
子数和检验效果归一化后的无量纲数值。
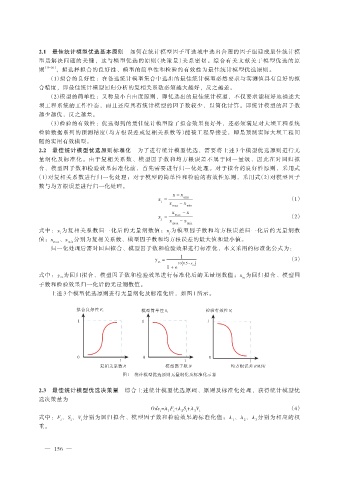
上述 3 个模型优选原则进行无量纲化及标准化后，如图 1 所示。

拟合良好性 F i
模型简单性 S i 检验有效性 V i
1 1 1

0 0 0
1 1 1
复相关系数 R 模型因子数 N 均方根误差 RMSE
图 1 统计模型优选原则无量纲化及标准化示意

2.3 最佳统计模型优选决策量 综合上述统计模型优选原理、原则及标准化处理，获得统计模型优
选决策量为
Odc =λ F +λ S +λ V i （4）
2 i
i
i
1
3
式中：F 、S 、V 分别为回归拟合、模型因子数和检验效果的标准化值；λ 、λ 、λ 分别为相应的权
i
i
i
2
1
3
重。
— 156 —