Page 39 - 2022年第53卷第2期

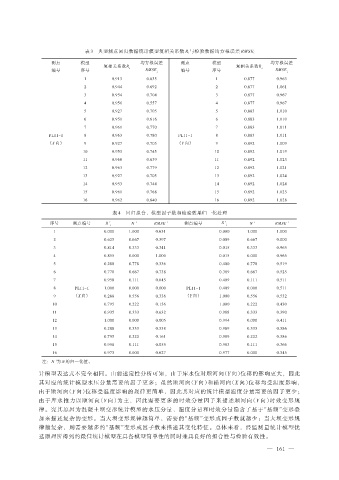
表 3 典型测点回归数据统计模型复相关系数 R i与检验数据均方根误差 RMSE i
测点 模型 均方根误差 测点 模型 均方根误差
复相关系数R i 复相关系数R i
编号 序号 RMSE i 编号 序号 RMSE i
1 0.913 0.635 1 0.877 0.963
2 0.944 0.692 2 0.877 1.061
3 0.954 0.704 3 0.877 0.967
4 0.956 0.557 4 0.877 0.967
5 0.927 0.705 5 0.883 1.010
6 0.951 0.616 6 0.883 1.010
7 0.961 0.770 7 0.883 1.011
PL11-1 8 0.963 0.780 PL11-1 8 0.883 1.011
（X 向） 9 0.927 0.705 （Y 向） 9 0.892 1.009
10 0.953 0.745 10 0.892 1.019
11 0.960 0.639 11 0.892 1.023
12 0.963 0.779 12 0.892 1.021
13 0.927 0.705 13 0.892 1.024
14 0.953 0.744 14 0.892 1.024
15 0.961 0.768 15 0.892 1.025
16 0.962 0.640 16 0.892 1.028
表 4 回归拟合、模型因子数和检验效果归一化处理
序号 测点编号 R ′ i N ′ RMSE ′ 测点编号 R ′ i N ′ RMSE ′
1 0.000 1.000 0.651 0.000 1.000 1.000
2 0.625 0.667 0.397 0.009 0.667 0.000
3 0.814 0.333 0.341 0.015 0.333 0.965
4 0.855 0.000 1.000 0.015 0.000 0.965
5 0.288 0.778 0.336 0.400 0.778 0.519
6 0.770 0.667 0.738 0.389 0.667 0.525
7 0.958 0.111 0.045 0.409 0.111 0.511
8 PL11-1 1.000 0.000 0.000 PL11-1 0.409 0.000 0.511
9 （X 向） 0.288 0.556 0.336 （Y 向） 1.000 0.556 0.532
10 0.795 0.222 0.156 1.000 0.222 0.430
11 0.935 0.333 0.632 0.988 0.333 0.390
12 1.000 0.000 0.005 0.994 0.000 0.411
13 0.288 0.333 0.338 0.989 0.333 0.386
14 0.795 0.222 0.161 0.989 0.222 0.386
15 0.958 0.111 0.055 0.983 0.111 0.366
16 0.973 0.000 0.627 0.977 0.000 0.345
注：N ′为 N 的归一化值。
计模型表达式不完全相同。由前述定性分析可知，由于库水位对顺河向（Y 向）位移的影响更大，因此
其对应的统计模型水压分量需要的因子更多；虽然顺河向（Y 向）和横河向（X 向）位移均受温度影响，
由于顺河向（Y 向）位移受温度影响的规律更简单，因此其对应的统计模型温度分量需要的因子更少；
由于库水推力以顺河向（Y 向）为主，因此需要更多的时效分量因子来描述顺河向（Y 向）时效变形规
律。究其原因为混凝土坝变形统计模型的水压分量、温度分量和时效分量隐含了基于“基频”变形叠
加来描述复杂的变形。当大坝变形规律越简单，需要的“基频”变形或因子数就越少；当大坝变形规
律越复杂，则需要越多的“基频”变形或因子数来描述其变化特征。总体来看，经监测量统计模型优
选原理所得到的最佳统计模型在具备模型简单性的同时兼具良好的拟合性与检验有效性。

— 161 —