Page 123 - 2022年第53卷第3期

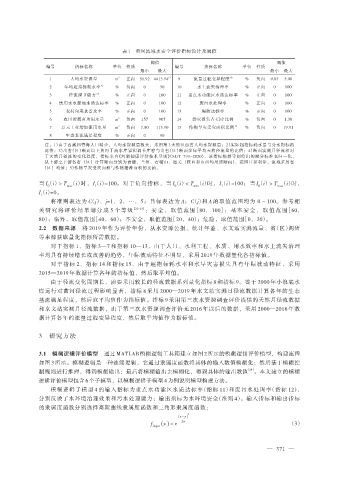
表 1 黄河流域水安全评价指标设计及阈值
阈值 阈值
编号 指标名称 单位 性质 编号 指标名称 单位 性质
最小 最大 最小 最大
1 人均水资源量 m 3 正向 51.92 4413.94 1） 9 流量过程变异程度 4） % 负向 0.05 5.00
2 年均超指标耗水率 2） % 负向 0 50 10 水土流失治理率 % 正向 0 100
3 径流调节能力 3） % 正向 0 100 11 重点水功能区水质达标率 % 正向 0 100
4 饮用水水源地水质达标率 % 正向 0 100 12 废污水处理率 % 正向 0 100
5 农村自来水普及率 % 正向 0 100 13 堤防达标率 % 正向 0 100
6 农田灌溉亩均用水量 m 3 负向 157 907 14 洪灾损失占 GDP 比例 % 负向 0 1.38
7 万元工业增加值用水量 m 3 负向 7.80 113.90 15 作物旱灾受灾面积比例 5） % 负向 0 19.91
8 生态基流满足程度 % 正向 0 90
注：1）由于西藏和青海人口稀少，人均水资源量极大，采用第 3 大的江西省人均水资源量；2）实际超指标耗水量与分水指标的
比值；3）出省（区）断面以上黄河干流水库累积调节库容与出省（区）断面多年平均天然径流量的比值；4）断面实测月径流相对
于天然月径流的变化程度，指标来自《河湖健康评估技术导则》（SL/T 793-2020），该指标根据导则给出的赋分标准表归一化，
从上游至下游各省 （区） 计算断面分别为贵德、兰州、石嘴山、潼关 （陕西和山西均用该断面）、花园口和利津，流域采用省
（区） 均值；5）作物旱灾受灾面积与作物播种面积的比值。

当 I（i）＞T （i）时，I（i）=100。对于负向指标，当 I（i）＜T （i）时，I（i）=100；当 I（i）＞T （i）时，
0 max 1 0 min 1 0 max
I（i）=0。
1
将准则表达为 C（j），j=1，2，…，5；目标表达为 A；C（j）和 A 的取值范围均为 0 ~ 100。参考相
关 研 究 将 评 价 结 果 划 分 成 5 个 等 级 ［22-23］ ： 安 全 ， 取 值 范 围［80， 100］； 基 本 安 全 ， 取 值 范 围［60，
80）；临界，取值范围［40，60）；不安全，取值范围［20，40）；危险，取值范围［0，20）。
2.2 数据来源 将 2019 年作为评价年份，从水资源公报、统计年鉴、水文站实测流量、省（区）调研
等来源获取量化指标所需数据。
对于指标 1、指标 3—7 和指标 10—13，由于人口、水利工程、水质、用水效率和水土流失治理
率均具有持续增长或改善的趋势，年际波动特征不明显，采用 2019 年数据量化各指标值。
对于指标 2、指标 14 和指标 15，由于超指标耗水率和水旱灾害损失具有年际波动特征，采用
2015—2019 年数据计算各年的指标值，然后取平均值。
由于径流变化周期长，需要采用较长的径流数据系列量化指标 8 和指标 9。鉴于 2000 年小浪底水
库运行对黄河径流过程影响显著，指标 8 采用 2000—2019 年水文站实测日径流数据计算各年的生态
基流满足程度，然后取平均值作为指标值。指标 9 采用第三次水资源调查评价提供的天然月径流数据
和水文站实测月径流数据，由于第三次水资源调查评价无 2016 年以后的数据，采用 2000—2016 年数
据计算各年的流量过程变异程度，然后取平均值作为指标值。

3 研究方法

3.1 模糊逻辑评价模型 通过 MATLAB模糊逻辑工具箱建立如图 2所示的模糊逻辑评价模型，构建流程
如图 3 所示。模糊逻辑是一种连续逻辑，它通过隶属度函数将具体的输入数值模糊化；然后基于模糊控
制规则进行推理，得到模糊输出；最后将模糊输出去模糊化，得到具体的输出数值 ［24］ 。本文建立的模糊
逻辑评价模型包含 6个子模型，以模糊逻辑子模型 4为例说明模型构建方法。
模糊逻辑子模型 4 的输入指标为重点水功能区水质达标率（指标 11）和废污水处理率（指标 12），
分别反映了水环境治理效果和污水处理能力；输出指标为水环境安全（准则 4）。输入指标和输出指标
的隶属度函数分别选择高斯曲线隶属度函数和三角形隶属度函数：
(x - p ) 2
f ( ) x = e 2σ （3）
input

— 371 —