Page 12 - 2022年第53卷第4期

表 3 滑移失稳计算参数
干湿循环 F s - s h w α c tanφ l W V U
0 2.58 472 0.64
5 2.51 426 0.63
15 2.45 65 7 383 0.62 28.61 150117.34 21125 9298.25
20 2.29 358 0.58
30 2.13 339 0.54

8
倾倒式失稳
滑移式失稳
6
稳定系数 4

2

0
0 5 10 15 20 25 30
干湿循环次数

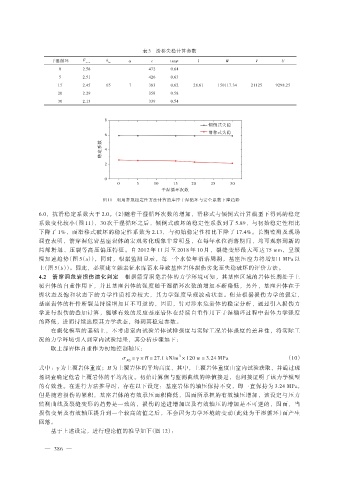
图 11 利用常规稳定性方法计算的库岸干湿循环与安全系数下降趋势
6.0，抗滑稳定系数大于 2.0。（2）随着干湿循环次数的增加，滑移式与倾倒式计算模型下得到的稳定
系数变化较小（图 11），30 次干湿循环之后，倾倒式破坏的稳定性系数到了 5.89，与初始稳定性相比
下降了 1%，而滑移式破坏的稳定性系数为 2.13，与初始稳定性相比下降了 17.4%。长期监测及现场
调查表明，箭穿洞危岩基座岩体的宏观劣化现象非常明显，在每年水位消落期间，均可观察到新的
局部坍塌、压裂等高压偏压特征。自 2012 年 11 月至 2018 年 10 月，裂缝变形最大可达 75 mm，呈缓
慢加速趋势（图 5（a）），同时，根据监测显示，每一个水位年消落周期，基座压应力将增加 1 MPa 以
上（图 5（b））。因此，必须建立能表征水库蓄水导致基座岩体损伤劣化至失稳破坏的评价方法。
4.2 箭穿洞危岩损伤演化判定 根据箭穿洞危岩体的力学环境可知，其基座区域的岩体长期处于上
覆岩体的自重作用下，并且基座岩体的强度随干湿循环次数的增加不断降低，另外，基座岩体在干
燥状态及饱和状态下的力学性质相差较大，其力学强度呈现波动状态。但是根据损伤力学的假定，
基座岩体的杆件断裂是持续增加且不可逆的，因而，针对涉水危岩体的稳定分析，通过引入损伤力
学进行损伤的叠加计算，能够有效的反应基座岩体在持续自重作用下干湿循环过程中岩体力学强度
的降低，进而持续追踪其力学状态，得到其稳定参数。
在概化模型的基础上，不考虑室内试验岩体试样强度与实际工况岩体强度的差异性，将实际工
况的力学环境引入到室内试验结果，其分析步骤如下：
取上部岩体自重作为初始控制轴压：
σ = γ × H = 27.1 kN/m × 120 m = 3.24 MPa （10）
3
E0
式中：γ 为上覆岩体重度；H 为上覆岩体的平均高度，其中，上覆岩体重度由室内试验获取，并通过现
场调查确定危岩上覆岩体的平均高度。初始计算值与监测曲线的峰值接近，也间接证明了该力学模型
的有效性。在进行方法推导时，存在以下设定：基座岩体的轴压保持不变，即一直保持为 3.24 MPa，
但是随着损伤的累积，基座岩体的有效承压面积降低，因而所承担的有效轴压增加，该设定与压力
监测曲线及裂缝变形的趋势是一致的，损伤的递进增加以及有效轴压的增加是不可逆的，因而，当
损伤变量及有效轴压提升到一个较高的值之后，不会因为力学环境的变动（此处为干湿循环）而产生
回落。
基于上述设定，进行理论值的推导如下（图 12）：

— 386 —