Page 126 - 2022年第53卷第8期
P. 126
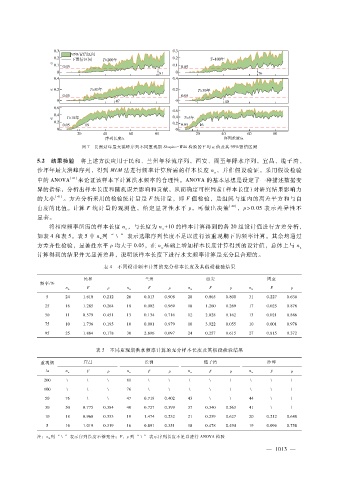
图 7 长洲站年最大洪峰序列不同重现期 Shapiro - Wilk检验的平均 α值及其 95%置信区间
5.2 结果检验 将上述方法应用于民和、兰州年径流序列,西安、周至年降水序列,宜昌、缆子湾、
沙坪年最大洪峰序列,得到 MLM法进行频率计算所需的样本长度 n,并作假设验证。采用假设检验
a
中的 ANOVA [41] 来论证该样本下计算洪水频率的合理性。ANOVA的基本思想是设定了一种描述数据变
异的指标,分析出样本长度和随机误差影响和贡献,从而确定可控因素(样本长度)对研究结果影响力
的大小 [41] 。方差分析采用的检验统计量是 F统计量,即 F值检验,是组间与组内的离差平方和与自
由度的比值。计算 F统计 量的 观测 值,给 定 显著性水 平 p,可做 出 决策 [42] ,p>0.05表示 差 异性不
显著。
将相应频率所需的样本长度 n,与长度为 n+ 10 的样本计算得到的各 20组设计值进行方差分析,
a a
如表 4和表 5。表 5中 n列 “\” 表示选取序列长度不足以进行该重现期下的频率计算。其余均通过
a
方差齐性检验,显著性水平 p均大于 0.05,在 n基础上增加样本长度计算得到的设计值,总体上与 n
a a
计算得到的结果并无显著差异,说明该样本长度下进行水文频率计算是充分且合理的。
表 4 不同设计频率计算的充分样本长度及其假设检验结果
民和 兰州 西安 周至
频率?%
F p F p F p F p
n a n a n a n a
5 24 1.610 0.212 26 0.013 0.908 28 0.065 0.800 31 0.227 0.636
25 16 1.285 0.264 18 0.002 0.969 18 1.260 0.269 17 0.025 0.876
50 11 0.579 0.451 13 0.134 0.716 12 2.028 0.162 13 0.021 0.886
75 10 1.736 0.195 10 0.001 0.979 10 3.922 0.055 10 0.001 0.978
95 25 1.884 0.178 30 2.896 0.097 24 0.257 0.615 27 0.815 0.372
表 5 不同重现期洪水频率计算的充分样本长度及其假设检验结果
重现期 宜昌 长洲 缆子湾 沙坪
?a n a F p n a F p n a F p n a F p
200 \ \ \ 81 \ \ \ \ \ \ \ \
100 \ \ \ 76 \ \ \ \ \ \ \ \
50 76 \ \ 47 0.719 0.402 43 \ \ 44 \ \
30 50 0.775 0.384 40 0.727 0.399 37 0.340 0.563 41 \ \
10 18 0.960 0.333 19 1.474 0.232 21 0.239 0.627 20 0.212 0.648
5 16 1.019 0.319 16 0.891 0.351 18 0.478 0.494 19 0.096 0.758
注:n a 列 “\” 表示序列长度不够充分;F、p列 “\” 表示序列长度不足以进行 ANOVA检验
0
— 1 1 3 —