Page 123 - 2022年第53卷第8期

进一步分析 ｋ值对设计值的影响，根据谢欣荣 ［３４］ ＧＥＶ分布离均系数的推导，当 ｋ ≠０时，频率 Ｐ
的计算公式为：
对应的离均系数 Ф Ｐ
ｋ
２
＝ ±｛ Γ （１ ＋ ｋ） － ［ － ｌｎ（１ － Ｐ）］｝?［ Γ （１ ＋ ２ｋ） － Γ（１ ＋ ｋ）］ １?２ （９）
Φ Ｐ
式中：ｋ＞０时，取正；ｋ＜０时，取负。
计算公式为：
当 ｋ ＝ ０ 时，频率 Ｐ对应的离均系数 Ф ｐ

＝－ ６｛０．５７７２２ ＋ ｌｎ［ － ｌｎ （１ － Ｐ）］｝? ! （１０）
Φ Ｐ 槡
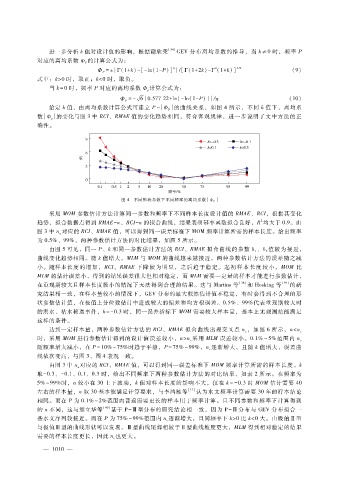
的曲线关系，如图 ４所示，不同 ｋ值下，离均系
给定 ｋ值，由离均系数计算公式可建立 Ｐ～ Ф Ｐ
的变化与图 ３中 ＲＣＩ、ＲＭＡＥ值的变化趋势相同，符合客观规律，进一步说明了文中方法的正
数 Ф ｐ
确性。

图 ４ 不同形状参数下不同频率的离均系数 Ф Ｐ
采用 ＭＯＭ参数估计方法计算同一参数和频率下不同样本长度设计值的 ＲＭＡＥ、ＲＣＩ，根据其变化
２
趋势，拟合数据点得到 ＲＭＡＥ － ｎ、ＲＣＩ － ｎ的拟合曲线，结果表明幂率函数拟合良好，Ｒ均大于 ０．９。由
图 ３中 ｎ对应的 ＲＣＩ、ＲＭＡＥ值，可以得到同一误差标准下 ＭＯＭ频率计算所需的样本长度。给出频率
ａ
为 ０．５％、９９％，两种参数估计方法的对比结果，如图 ５所示。
由图 ５可见，同一 Ｐ、ｋ和同一参数估计方法的 ＲＣＩ、ＲＭＡＥ拟合曲线的参数 ｂ、ｂ值较为接近，
１
２
曲线变化趋势相同。随 ｋ值增大，ＭＬＭ与 ＭＯＭ的曲线越来越接近，两种参数估计方法的误差随之减
小。随样本长度的增加，ＲＣＩ、ＲＭＡＥ下降较为明显，之后趋于稳定。起初 样本 长度 较 小，ＭＯＭ 比
ＭＬＭ的估计误差小，得到的结果误差很大但相对稳定，而 ＭＬＭ需要一定量的样本才能进行参数估计，
在重现期较大且样本长度极小的情况下无法得到合理的结果。这与 Ｍａｒｔｉｎｓ等 ［３８］ 和 Ｈｏｓｋｉｎｇ等 ［３９］ 的研
究结果相一致，在样本量较小的情况下，ＧＥＶ分布的最大似然估计值不稳定，有时会得到不合理的形
状参数估计值，在极值上分位数估计中造成较大的偏差和均方根误差。０．５％、９９％代表重现期较大时
的洪水、枯水稀遇事件，ｋ ＝－ ０．３ 时，同一误差指标下 ＭＯＭ需要较大样本量，基本上无观测站能满足
这样的条件。
达到一定样本量，两种参数估计方法的 ＲＣＩ、ＲＭＡＥ拟合曲线出现交叉点 ｎ，如图 ６所示，ｎ＜ｎ ｃ
ｃ
时，采用 ＭＯＭ进行参数估计得到的设计值误差较小，ｎ＞ｎ采用 ＭＬＭ误差较小。０．１％～５％范围内 ｎ
ｃ ｃ
随频率增大减小，在 Ｐ ＝ １０％～７５％时趋于平稳，Ｐ ＝ ７５％～９９％，ｎ逐渐增大，且随 ｋ值增大，误差曲
ｃ
线依次变高，与图 ３、图 ４表现一致。
由图 ３中 ｎ对应的 ＲＣＩ、ＲＭＡＥ值，可以得到同一误差标准下 ＭＯＭ 频率计算所需的样本长度。ｋ
ａ
取－ ０．３、－ ０．１、０．１、０．３时，给出不同频率下两种参数估计方法的对比结果，如表 ２所示。在频率为
５％～９９％时，ｎ较小在 ３０上下波动，ｋ值对样本长度的影响不大，仅在 ｋ ＝－ ０．３时 ＭＯＭ估计需要 ４０
左右的样本量，ｎ取 ３０基本能满足计算要求，与李鸿雁等 ［１２］ 认为水文频率计算需要 ３０年的样本结论
相同。而在 Ｐ为 ０．１％～２％范围内普遍需要更长的样本用于频率计算。且不同参数和频率下计算得到
的 ｎ不同，这与熊立华等 ［４０］ 基于 Ｐ － Ⅲ型分布的研究结论相一致，因为 Ｐ － Ⅲ分布与 ＧＥＶ分布拟合一
些水文序列较接近。而在 Ｐ为 ７５％～９９％范围内 ｎ逐渐增大，且同频率下 ｋ＞０比 ｋ＜０大。由极值Ⅱ型
ｃ
与极值Ⅲ型的曲线形状可以发现，Ⅲ型曲线尾部相较于Ⅱ型曲线坡度更大，ＭＬＭ得到相对稳定的结果
需要的样本长度更长，因此 ｎ也更大。
ｃ
１
— １ ０ ０ —