Page 21 - 2022年第53卷第8期

ｖ＝ Ａ?（１ ＋ Ｃｅ ） ＋ Ｂ （５）
Ｄ １ θ ａ
ｒ １
为气温。Ａ ＋ Ｂ为冰－ 气－
式中：ｖ为雷达波速，其中用 ｖ和 ｖ分别代表粒状冰和柱状冰的雷达波速；θ ａ
ｒ ｒｇ ｒｃ
泥沙三相黄河冰的雷达波速，Ｂ为纯水－ 泥沙二相黄河水的雷达波速，Ａ，Ｂ由理论指导，通过统计优
化所得；Ｃ 为调节系数，Ｄ 为曲线逻辑增长率，它们均由实测数据统计所得。选择式（５）的目的就是
１
１
为了涵盖黄河冻结平封冰、立封冰、冰花冰和未完全冻结的冰花、冰塞冰坝中破碎冰块，同时保证雷
达波速遵循物理基础，见图 ６（ｂ）。具体气温与含未冻水粒状冰、柱状冰的雷达波速统计结果由图 ７
给出。

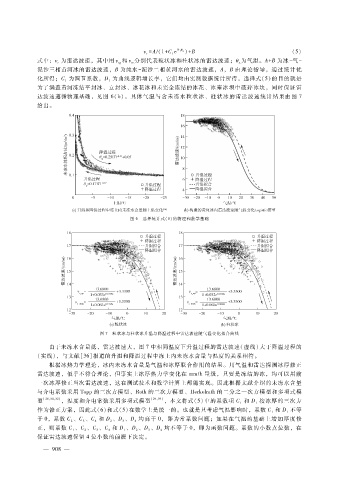
图 ６ 选择统计式（５）的物理和数学基础

图 ７ 粒状冰与柱状冰升温与降温过程中雷达波速随气温变化拟合曲线

由于未冻水含量低，雷达波速大，图 ７中相同温度下升温过程的雷达波速（虚线）大于降温过程的
（实线），与文献［３６］报道的升温和降温过程中冻土内未冻水含量与温度的关系相符。
根据冰热力学理论，冰内未冻水含量是气温和冰厚联合作用的结果。用气温和雷达探测冰厚修正
雷达波速，似乎不符合理论，但事实上冰厚热力学变化在 ｍｍ?ｈ量级，只要是冻结的冰，均可以用前
一次冰厚修正当次雷达波速，这在测试技术和数学计算上都能实现。因此根据文献介绍的未冻水含量
与介电系数采用 Ｔｏｐｐ的三次方模型、Ｒｏｔｈ的三次方模型、Ｈｅｒｋｅｌｒａｔｈ的二分之一次方模型和多项式模
型 ［２８，３０，３２］ ，温度和介电常数采用多项式模型 ［２９，３９］ ，本文将式（５）中的系数项 Ｃ 和 Ｄ 按冰厚的三次方
１
１
作为修正方案，因此式（ ６）和式（５）在数学上是统一的。也就是只考虑气温影响时，系数 Ｃ 和 Ｄ 不等
１ １
于 ０，系数 Ｃ、Ｃ、Ｃ 和 Ｄ、Ｄ、Ｄ 均高于 ０，即为常系数问题；如果在气温的基础上增加厚度修
２ ３ ４ ２ ３ ４
正，则系数 Ｃ、Ｃ、Ｃ、Ｃ 和 Ｄ、Ｄ、Ｄ、Ｄ 均不等于 ０，即为函数问题。系数的小数点位数，在
１ ２ ３ ４ １ ２ ３ ４
保证雷达波速保留 ４位小数的前提下决定。
８
— ９ ０ —