Page 64 - 2022年第53卷第8期

ｓ ＝ σ （ｎｅｔ） ＝ σ （ｗ·ｈ ＋ ｗ·ｘ ＋ ｂ） （２）
ｔ ｔ ｈ ｔ － １ ｘ ｔ
ａ＝ ｔａｎｈ （ｎｅｔ） ＝ｔａｎｈ （ｗ·ｈ ＋ ｗ·ｘ ＋ ｂ） （３）
ｔ ｔ ｈ ｔ － １ ｘ ｔ
（ ２）更新单元状态
Ｃ＝ ｓ Ｃ ＋ （１ － ｓ） ａ ｔ （４）
ｔ － １
ｔ
ｔ
ｔ
（ ３）计算隐藏层输出
ｈ＝ ｓ ｔａｎｈ（Ｃ） （５）
ｔ
ｔ
ｔ
（ ４）输出预测值
ｙ＝ σ （ｚ） ＝ σ （ｗ·ｈ＋ ｂ） （６）
ｔ ｔ ｙ ｔ ｙ
式中：ｘ、ｓ和 ａ分别为当前时段输入层输入、共享门和信息状态；Ｃ 和 Ｃ分别为前一时段和当前时
ｔ ｔ ｔ ｔ － １ ｔ
段的单元状态；ｈ 和 ｈ分别为前一时段和当前时段隐藏层输出；ｙ为当前时段输出层的输出，也是当
ｔ － １
ｔ
ｔ
前时段的预测值；ｎｅｔ和 ｚ为中间变量，没有具体含义；［ｗ，ｗ，ｂ］和［ｗ，ｂ］分别为隐藏层和输出
ｔ
ｙ
ｙ
ｈ
ｘ
ｔ
层权重变量，也是整个神经网络模型需要训练的变量；符号·和符号分别表示矩阵乘法和矩阵元素
间乘法。函数 σ （·）和 ｔａｎｈ（·）分别是 ｓｉｇｍｏｉｄ和 ｔａｎｈ激活函数。
为提升神经网络类模型性能并避免产生过拟合现象，在模型训练过程中增加小批量梯度下降、正
则化、衰减学习率和 ｄｒｏｐｏｕｔ等机制。
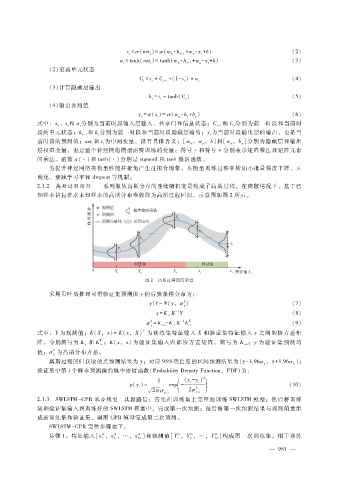
２．１．２ 高斯过程回归 一系列服从高斯分布的连续随机变量构成了高斯过程。在离散情况下，基于已
知样本信息推求未知样本的高斯分布参数即为高斯过程回归，示意图如图 ２所示。

图 ２ 高斯过程回归示意

采用贝叶斯推理可得验证集预测值 ｙ的后验条件分布为：
２
ｙＹ～Ｎ（ 珋 ） （７）
ｙ，σ ｙ
ｙ  － １ （８）
珋 ＝ Ｋ Ｋ Ｙ
２ － １ Ｔ
σ ｙ ＝ Ｋ － Ｋ Ｋ Ｋ  （９）


Ｔ
式中：Ｙ为观测值；Ｋ（Ｘ，ｘ） ＝Ｋ（ｘ，Ｘ） 为训练集特征输入 Ｘ和验证集特征输入 ｘ之间的协方差矩
Ｔ
阵，分别简写为 Ｋ 和 Ｋ ；Ｋ（ｘ，ｘ）为验证集输入内部协方差矩阵，简写为 Ｋ ； 珋 验证集预测均
ｙ为
  
２
值；σ ｙ 为高斯分布方差。
高斯过程回归获取的点预测结果为 珋 ｙ ，ｙ ］；
ｙ；对应 ９５％置信度的区间预测结果为［ 珋 － １ ．９６ σ ｙ 珋 ＋ １ ．９６ σ ｙ
验证集中第 ｉ个样本预测值的概率密度函数（ＰｒｏｂａｂｉｌｉｔｙＤｅｎｓｉｔｙＦｕｎｃｔｉｏｎ，ＰＤＦ）为：
ｙ）
(
１ （ｙ － 珋 ２
ｉ
ｉ
ｐ（ｙ） ＝ ｅｘｐ－ ２ ) （１０）
ｉ
槡 ２ πσ ｙ，ｉ ２ σ ｙ，ｉ
２．１．３ ＳＷＬＳＴＭ－ ＧＰＲ混合模型 其思路是：首先在训练集上完整地训练 ＳＷＬＳＴＭ 模型；然后将训练
集和验证集输入到训练好的 ＳＷＬＳＴＭ模型中，完成第一次预测；最后将第一次预测结果与观测值重组
成新训练集和验证集，调用 ＧＰＲ模型完成第二次预测。
ＳＷＬＳＴＭ－ ＧＰＲ完整步骤如下：
ｔａ
ｔａ
ｔａ
ｔａ
ｔａ
ｔａ
步骤 １：特征输入［ｘ，ｘ，…，ｘ ］和观测值［Ｙ ，Ｙ ，…，Ｙ ］构成第一次训练集，用于训练
１ ２ Ｔａ １ ２ Ｔａ
— ９ ５ １ —