Page 66 - 2022年第53卷第8期

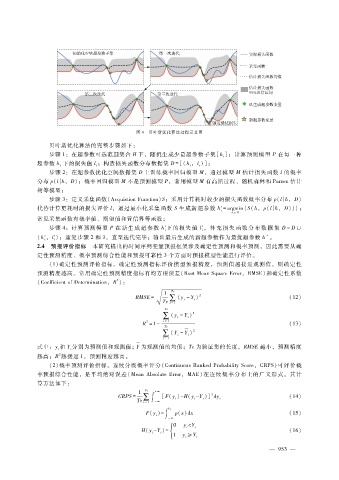
图 ４ 贝叶斯优化算法过程示意图
贝叶斯优化算法的完整步骤如下：
步骤 １：在超参数可选范围集合 Ｈ下，随机生成少量超参数子集［ｈ］；计算预测模型 Ｐ在每一种
ｉ
超参数 ｈ下的损失值 ｌ；构造损失函数分布数据集 Ｄ ＝ ［（ｈ，ｌ）］；
ｉ ｉ ｉ ｉ
步骤 ２：在超参数优化空间数据集 Ｄ上训练概率回归模型 Ｍ，通过模型 Ｍ 估计损失函数 ｌ的概率
分布 ｐ（ｌｈ，Ｄ）；概率回归模型 Ｍ不是预测模型 Ｐ，常用模型 Ｍ有高斯过程、随机森林和 Ｐａｒｚｅｎ估计
树等模型；
步骤 ３：定义采集函数（ＡｃｑｕｉｓｔｉｏｎＦｕｎｃｔｉｏｎ）Ｓ；采用计算耗时较少的损失函数概率分布 ｐ（ｌｈ，Ｄ）
代替计算更耗时的损失评价 ｌ，通过最小化采集函数 Ｓ生成新超参数 ｈ′ ＝ ａｒｇｍｉｎ ｛Ｓ（ｈ，ｐ（ｌｈ，Ｄ））｝；
ｉ
ｈ ∈Ｈ
常见采集函数有概率值、期望值和置信界等函数；
步骤 ４：计算预测模型 Ｐ在 新生 成超 参数 ｈ′下的损 失 值 ｌ′，补 充 损 失 函 数 分 布 数 据 集 Ｄ＝ Ｄ ∪
ｉ ｉ

（ｈ′，ｌ′）；重复步骤 ２和 ３，直至迭代完毕；输出最后生成的新超参数作为最优超参数 ｈ 。
ｉ ｉ
２．４ 预报评价指标 本研究提出的时间序列变量预报框架涉及确定性预测和概率预测，因此需要从确
定性预测精度、概率预测综合性能和预报可靠性 ３个方面对预报模型性能进行评价。
（１）确定性预测评价指标。确定性预测指标评价模型预报精度，预测值越接近观测值，则确定性
预测精度越高。常用确定性预测精度指标有均方根误差（ＲｏｏｔＭｅａｎＳｑｕａｒｅＥｒｒｏｒ，ＲＭＳＥ）和确定性系数
２
（ＣｏｅｆｆｉｃｉｅｎｔｏｆＤｅｔｅｒｍｉｎａｔｉｏｎ，Ｒ）：
１ Ｔｅ
ＲＭＳＥ ＝ ∑ （ｙ－ Ｙ） ２ （１２）
槡
ｉ
ｉ
Ｔｅ ｉ ＝１
Ｔｅ
∑ （ｙ－ Ｙ） ２
ｉ
ｉ
２
Ｒ ＝ １ － ｉ ＝１ （１３）
Ｔｅ
∑ （Ｙ－ Ｙ） ２
ｉ
ｉ
ｉ ＝１
式中：ｙ和 Ｙ分别为预测值和观测值；Ｙ为观测值的均值；Ｔｅ为验证集的长度。ＲＭＳＥ越小，预测精度
ｉ
ｉ
２
越高；Ｒ越接近 １，预测精度越高。
（２）概率预测评价指标。连续分级概率评分（ＣｏｎｔｉｎｕｏｕｓＲａｎｋｅｄＰｒｏｂａｂｉｌｉｔｙＳｃｏｒｅ，ＣＲＰＳ）可评价概
率预报综合性能，是平均绝对误差（ ＭｅａｎＡｂｓｏｌｕｔｅＥｒｒｏｒ，ＭＡＥ）在连续概率分布上的广义形式。其计
算方法如下：
１ Ｔｅ ＋ ∞
２
ＣＲＰＳ ＝ ∑∫ ［Ｆ（ｙ） － Ｈ（ｙ － Ｙ）］ｄｙ ｉ （１４）
ｉ
ｉ
ｉ
Ｔｅ ｉ ＝１ － ∞
ｙ ｉ
ｉ ∫
Ｆ（ｙ） ＝ ｐ（ｘ）ｄｘ （１５）
－ ∞
{ ０ ｙ＜Ｙ ｉ
ｉ
Ｈ（ｙ － Ｙ） ＝ （１６）
ｉ
ｉ
１ ｙ ≥Ｙ
ｉ ｉ
— ９ ５ ３ —