Page 65 - 2022年第53卷第8期

ＳＷＬＳＴＭ模型；
ｔａ
ｔａ
ｔａ
ｔｅ
ｔｅ
ｔｅ
步骤 ２：训练集特征输入［ｘ，ｘ，…，ｘ ］和验证集特征输入［ｘ，ｘ，…，ｘ ］分别输入到训练
１ ２ Ｔａ １ ２ Ｔｅ
ｔａ
ｔａ
ｔａ
完毕的 ＳＷＬＳＴＭ模型中，完成第一次预测，得到训练集第一次预测结果［ｙ ，ｙ ，…，ｙ ］和验证
１ ，１
１ ，２
１ ，Ｔａ
ｔｅ
ｔｅ
ｔｅ
集第一次预测结果［ｙ ，ｙ ，…，ｙ ］；
１，１ １，２ １，Ｔｅ
ｔａ
ｔａ
ｔａ
ｔａ
ｔａ
ｔａ
步骤 ３：训练集第一次预测结果［ｙ ，ｙ ，…，ｙ ］和观测值［Ｙ ，Ｙ ，…，Ｙ ］构成第二次训
１ ，１ １ ，２ １ ，Ｔａ １ ２ Ｔａ
ｔｅ
ｔｅ
ｔｅ
练集，将验证集第一次预测结果［ｙ ，ｙ ，…，ｙ ］作为第二次预测特征输入，调用 ＧＰＲ模型，得
１ ，Ｔｅ
１ ，２
１ ，１
ｔｅ
ｔｅ
ｔｅ
到验证集第二次预测结果［ ｙ ，ｙ ，…，ｙ ］；
２，２
２，Ｔｅ
２，１
ｔｅ
ｔｅ
ｔｅ
ｔｅ
ｔｅ
ｔｅ
步骤 ４：验证集第二次预测结果［ｙ ，ｙ ，…，ｙ ］和验证集观测值［Ｙ ，Ｙ ，…，Ｙ ］用来评
２，１ ２，２ ２，Ｔｅ １ ２ Ｔｅ
价模型的预测精度和可靠性。
步骤中 ｘ表示特征输入；ｙ 表示第一次预测结果，由 ＳＷＬＳＴＭ 模型得到；ｙ 表示第二次预测结
２，ｔ
ｔ
１，ｔ
果，由 ＧＰＲ模型得到；Ｙ表示观测值；上标 ｔａ和 ｔｅ分别代表训练集和验证集标识；Ｔａ和 Ｔｅ分别是训
ｔ
练集和验证集总样本数。
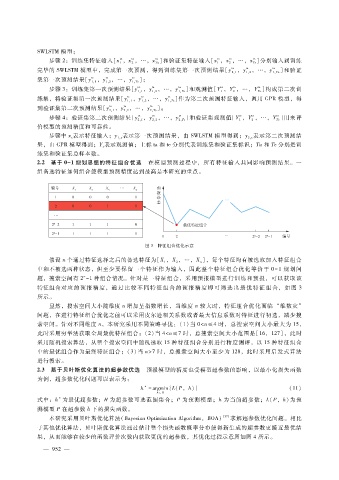
２．２ 基于 ０ － １规划思想的特征组合优选 在模型预测过程中，所有特征输入共同影响预测结果。一
组备选特征如何组合使模型预测精度达到最高是本研究的重点。
图 ３ 特征组合优化示意
假设 ｎ个通过特征选择之后的备选特征为［Ｘ，Ｘ，…，Ｘ］，每个特征均有被选取加入特征组合
ｎ
１
２
中和不被选两种状态，但至少要保留一个特征作为输入，因此整个特征组合优化等价于 ０ － １规划问
ｎ
题，搜索空间有 ２－ １种组合情况。针对某一特征组合，采用预报模型进行训练和预报，可以获取该
特征组合对应 的 预 报 精 度，通 过 比 较 不 同 特 征 组 合 的 预 报 精 度 即 可 筛 选 出 最 优 特 征 组 合，如 图 ３
所示。
显然，搜索空间大小随维度 ｎ增加呈指数增长，当维度 ｎ较大时，特征组合优化面临 “维数灾”
问题，在进行特征组合优化之前可以采用皮尔逊相关系数或者最大信息系数对特征进行初选，减少搜
索空间。针对不同维度 ｎ，本研究采用不同策略寻优：（１）当 ０＜ｎ ≤４时，总搜索空间大小最大为 １５，
此时采用穷举法获取全局最优特征组合；（２）当 ４＜ｎ ≤７时，总搜索空间大小范围是［１６，１２７］，此时
采用随机搜索算法，从整个搜索空间中随机选取 １５种特征组合分别进行精度测评，以 １５种特征组合
中的最优组合作为最终特征组合；（ ３）当 ｎ＞７时，总搜索空间大小至少为 １２８，此时采用启发式算法
进行搜索。
２．３ 基于贝叶斯优化算法的超参数优选 预报模型的精度也受模型超参数的影响，以最小化损失函数
为例，超参数优化问题可以表示为：

ｈ ＝ ａｒｇｍｉｎ ｛Ｌ（Ｐ，ｈ）｝ （１１）
ｈ ∈Ｈ

式中：ｈ 为最优超参数；Ｈ为超参数可选范围集合；Ｐ为预测模型；ｈ为当前超参数；Ｌ（Ｐ，ｈ）为预
测模型 Ｐ在超参数 ｈ下的损失函数。
本研究采用贝叶斯优化算法（ ＢａｙｅｓｉａｎＯｐｔｉｍｉｚａｔｉｏｎＡｌｇｏｒｉｔｈｍ，ＢＯＡ） ［３７］ 求解超参数优化问题。相比
于其他优化算法，贝叶斯优化算法通过估计整个损失函数概率分布使得新生成的超参数更接近最优结
果，从而能够在较少的函数评价次数内获取更优的超参数，其优化过程示意图如图 ４所示。
２
— ９ ５ —