Page 64 - 2022年第53卷第10期

中，二维图像的分割结果不可避免的会与原始图像间存在一定的差异，此外土石坝料的三维体积重构
也是基于一定的假设基础上建立的，因此通过数字图像识别出的级配曲线与施工现场挖坑检测得到的
试验级配曲线之间存在一定的误差。为了修正两者之间的误差，提高坝料级配智能检测结果的准确
性，本文通过对碾压结束后挖坑检测位置处拍摄的坝料图像识别得到的级配曲线与实际挖坑筛分得到
的级配曲线进行对比分析，建立了基于 ＢＰ神经网络的级配修正模型。
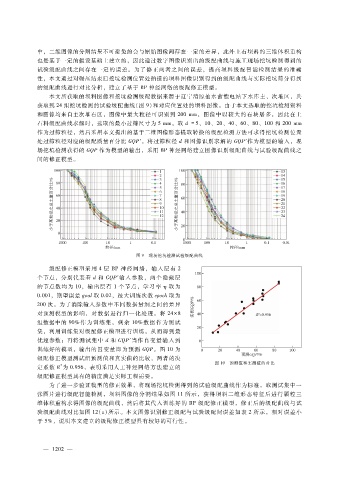
本文所获取的坝料图像和挖坑检测级配数据来源于辽宁清原抽水蓄能电站下水库主、次堆区，共
获取到 ２４组挖坑检测的试验级配曲线（图 ９）和对应位置处的坝料图像。由于本文选取的挖坑检测资料
和图像均来自主次堆石区，图像中最大粒径可识别到 ２００ｍｍ，图像中以较大的石块居多，因此在土
石料级配曲线求解时，选取的最小过筛尺寸为 ５ｍｍ，取 ｄ＝ ５ 、１０、２０、４０、６０、８０、１００和 ２００ｍｍ
作为过筛粒径，然后采用本文提出的基于二维图像形态提取转换的级配检测方法可求得挖坑检测位置
处过筛粒径对应的级配质量百分比 ＧＱＰ′，将过筛粒径 ｄ和图像识别求解的 ＧＱＰ′作为模型的输入，现
场挖坑检测获得的 ＧＱＰ作为模型的输出，采用 ＢＰ神经网络建立图像识别级配曲线与试验级配曲线之
间的修正模型。

图 ９ 现场挖坑检测试验级配曲线
级配修正模型采用 ４层 ＢＰ神经网络，输入层有 ２
个节点，分别代表着 ｄ和 ＧＱＰ′输入参数，两个隐藏层
的节点数均为 １０，输出层有 １个节点，学习率 η取为
０．００１，期望误差 ｇｏａｌ取 ０．０２，最大训练次数 ｅｐｏｃｈ取为
２００次。为了消除输入参数中不同数据量纲之间的差异
对预测模型的影响，对数据进行归一化处理。将 ２４ × ８
组数据中的 ９０％作为训练集，剩余 １０％数据作为测试
集，利用训练集对级配修正模型进行训练，从而得到最
优超参数；再将测试集中 ｄ和 ＧＱＰ′当作自变量输入到
训练好的模型，输出的因变量即为预测 ＧＱＰ。图 １０为
级配修正模型测试组预测值和真实值的比较，两者的决
图 １０ 预测值和实测值的对比
２
定系数 Ｒ为 ０．９５６，表明采用人工神经网络方法建立的
级配修正模型具有的精度满足实际工程需要。
为了进一步验证模型的修正效果，将现场挖坑检测得到的试验级配曲线作为标准，取测试集中一
张图片进行级配智能检测，坝料图像的分割结果如图 １１所示，获得坝料二维形态特征后进行颗粒三
维体积重构求得图像的级配曲线，然后将其代入训练好的 ＢＰ级配修正模型，修正后的级配曲线与试
验级配曲线对比如图 １２（ａ）所示。本文图像识别修正级配与试验级配间误差如表 ２所示，相对误差小
于 ５％，说明本文建立的级配修正模型具有较好的可行性。

— １ ２ ２ —
０