Page 32 - 2023年第54卷第2期

表 ６ Ｍε － ＯＩＤＥ算法与 Ｚ － ε － ＤＥ算法、ＴＳ － ε － ＤＥ算法求解防洪调度结果统计对比
削峰率?％
方法
Ｍ ε － ＯＩＤＥ ＴＳ － ε － ＤＥ Ｚ － ε － ＤＥ
潘家口 ６０．０８ ５１．０７ ５０．９２
大黑汀 ２３．９２ １４．３８ ２１．７２
水库、下游控制点
桃林口 ４５．２９ ４４．１９ ４５．７０
滦县 ３３．２６ ３２．０３ ３０．０４

图 ６ 潘家口水库使用 ＰＳＯ算法调度过程 图 ７ 潘家口水库使用 ＦＡ算法调度过程

５．５ 参数设置对 Ｍε － ＯＩＤＥ算法的影响 Ｍ ε － ＯＩＤＥ算法中控制参数 ＣＬ的确定，对水库防洪调度模型
求解有很大的影响。为了进行比较和验证，该算法使用不同的 ＣＬ值独立运行 １０次，其他参数和表 ４
保持一致。记录不同参数的防洪调度结果，结果见表 ７。
表 ７ Ｍε － ＯＩＤＥ算法采用不同参数的比较

削峰率?％
参数
ＣＬ ＝ ｉｎｆ ＣＬ ＝ １ ＣＬ ＝ ０
潘家口 ６０．０８ ５４．３１ ５４．３１
大黑汀 ２３．９２ １４．５８ １４．５８
水库、下游控制点
桃林口 ４５．２９ ４６．３７ ４６．３７
滦县 ３３．２６ ２８．３２ ２８．３２

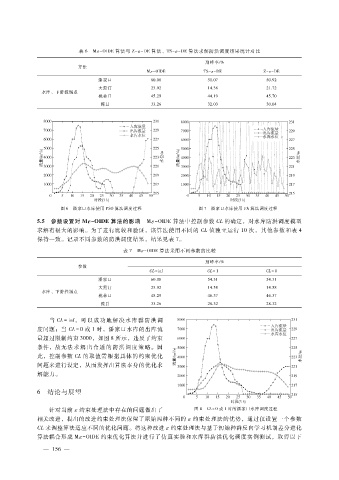
当 ＣＬ ＝ ｉｎｆ ，可以 成功 地解决 水库 群防 洪 调
度问题；当 ＣＬ ＝ ０ 或 １时，潘家口水库的出库流
量超过限制约束 ３０００，如图 ８所示，违反了约束
条件，故无法 求 解 出 合 适 的 防 洪 调 度 策 略。因
此，控制参数 ＣＬ的取值需根据具体的约束优化
问题来进行设定，从而发挥出算法本身的优化求
解能力。

６ 结论与展望

针对当前 ε 约束处理法中存在的问题做出了 图 ８ ＣＬ ＝ ０或 １时的潘家口水库调度过程
相关改进，提出的改进约束处理法保留了原始两种不同的 ε约束处理法的优势，通过仅设置一个参数
ＣＬ来调整算法适应不同的优化问题。将这种改进 ε 约束处理法与基于初始种群反向学习机制差分进化
算法耦合形成 Ｍ ε － ＯＩＤＥ约束优化算法并进行了仿真实验和水库群防洪优化调度实例测试，取得以下

— １ ５ —
６