Page 128 - 2023年第54卷第5期

对系统振荡特性更敏感，由尾水隧洞 － 下游调压室系统引起转速尾波振荡频率更低，衰减指数更小。
相较上游调压室面积，尾水调压室面积为设计面积的 ５０％时，转速尾波快速发散，小波动系统振荡失
稳，原因在于尾水隧洞长度远长于引水隧洞长度，水流惯性时间常数更大，对于小波动系统稳定性更不
利，需要更大调压室面积来抑制室内水体的波动，进而降低机组转速尾波低频振荡带来的不利影响。
４．４ 水轮机调速系统参数对小波动振荡稳定性影响 利用
式（ ２３），采用遍历法求解该抽水蓄能电站输水发电系统的
稳定域，由于调速器参数 ｂ 和 Ｔ 对于小波动系统的稳定性
ｐ
ｎ
影响较小，通常以 Ｔ 和 ｂ为双坐标的曲线描述系统的稳定
ｄ ｔ
性，曲线右侧为系统的稳定区域，左侧为系统的失稳区域，
如图 ５所示。在图 ５中选取稳定区域内的调速器参数组合
Ａ（７，０．８）、Ｂ（６，０．５）以及失稳区域内的调速器参数组合
Ｃ（３，０．３），分析调速器参数取值对于系统小波动振荡特性
图 ５ 系统小波动稳定域
的影响。通过求解 ３组不同调速器参数组合下的状态矩阵
，统计反应系统振荡环节的共轭复根，结果如表 ５。
Ｍ 的特征值 λ ｋ

表 ５ 不同调速器参数组合下状态矩阵 Ｍ 的共轭特征值 λ ｋ
共轭复根 λ ｋ
（Ｔ ｄ ，ｂ ｔ ）
λ ２，３ λ ４，５ λ ７，８ λ ９，１０
Ａ（７，０．８） － ０ ．２４８±０．１９４ｊ － ０ ．１２０±０．０４９ｊ － ０ ．００２±０．０４３ｊ ０ － ０ ．００４±０．０５６ｊ
０
０
０
Ｂ（６，０．５） － ０．１７０±０．３０９ｊ － ０．１６０±０．０９２ｊ － ０．００２±０．０４３ｊ ０ － ０．００４±０．０５７ｊ
０
０
０
Ｃ（３，０．３） ０．０２６±０．４２４ｊ － ０ ．２０７±０．２９５ｊ － ０ ．００２±０．０４３ｊ ０ － ０ ．００４±０．０５７ｊ
０
０
０
＝ ０ ．０２６±０．４２４ｊ，其他三对共轭
０
由表 ５可知，水轮机调速器参数组合为 Ｃ（３，０．３）时，特征值 λ ２，３
模
复根实部均为负值，小波动下系统振荡发散且失稳。通过状态矩阵特征值可以判断系统失稳由 λ ２，３
引起的振荡环节 Ｓ受水轮机调速系统和压力管道流量
１
态引起。由 ４．２节中的相关因子分析法可知 λ ２，３
变化的影响，因此取较小的水轮机调速器参数组合不利于小波动系统振荡稳定性。从 Ａ、Ｂ和 Ｃ三组
几乎不变，改变调速器参数对机组转速
调速器组合对应的特征值可知，调速器参数增大，λ ７，８ 和 λ ９，１０
对应的转速主波振荡角频率从 ０．４２４降至 ０．１９４ｒａｄ?ｓ，衰减指数由 ０．１７０增大至
尾波振荡无影响；λ ２，３
对应的振荡环节 Ｓ 的衰减指数由 ０．２０７降至０．１２０，振荡角频率从 ０．２９５降至 ０．０４９ｒａｄ?ｓ。
０．２４８；λ ４，５ ２
可见增大调速器参数有利于高频振荡环节 Ｓ稳定性，但对于中频振荡环节 Ｓ而言，此时的振荡角频率
２
１
和衰减指数变化趋势一致。故在小波动调节过程中需综合考虑选择合适的水轮机调速器参数。
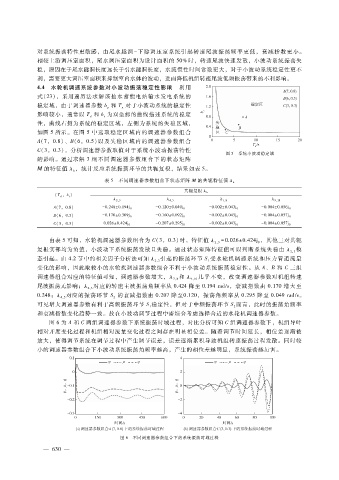
图 ６为 Ａ和 Ｃ两组调速器参数下系统振荡时域过程，对比分析可知 Ｃ组调速器参数下，机组导叶
相对开度变化过程和机组相对流量变化过程之间存在明显相位差。随着调节时间延长，相位差逐渐被
放大，使得调节系统在调节过程中产生调节误差，误差逐渐累积导致机组转速振荡过程发散。同时较
小的调速器参数组合下小波动系统振荡角频率越高，产生的相位差越明显，系统振荡越厉害。

图 ６ 不同调速器参数组合下的系统振荡时域过程
０
— ６ ３ —