Page 124 - 2023年第54卷第5期

ｆ（ λ ） ＝ λ Ｅ － Ｍ ＝ ０ （２４）
式中：λ为矩阵 Ｍ 的特征值；Ｅ为 １０阶单位矩阵。
方程（２４）的阶数为 １０，矩阵 Ｍ 相对应有 １０个特征值，故式（２４）可写成式（２５）：
１０
９
ａ λ ＋ ａλ ＋ …＋ ａλ ＋ ａ＝ ０ （２５）
９
０
１
１０
式中：ａ，ａ，ａ，…，ａ 为方程系数，由式（２４）中的行列式 λ Ｅ － Ｍ 展开求得。
０ １ ２ １０
（ｋ ＝ １ ，２，…，１０），进而研究系统发生小波动时的振荡
通过求解式（２５）可以得到系统的特征值 λ ｋ
特性，同时利用四阶龙格库塔法求解式（ ２３）得到抽水蓄能电站输水发电系统小波动下的振荡时域过程。
４ 系统小波动稳定性分析
４．１ 数学模型验证 由于图 １中的输水发电系统小波动稳定分析的数学模型高达 １０阶，为了避免在
推导过程中出现错误，确保小波动数学模型的正确性，采用四阶龙格库塔法求解式（ ２３）得到系统振荡
时域过程，同时与基于特征线法 ［２１］ 的数值模拟得到的系统振荡时域过程进行对比。本文计算采用的工
况：两台机组额定水头、额定流量和额定出力运行，分别受到 １０％的负荷扰动。机组在初始稳态工况
点的参数如表 ２，水轮机调速器参数 ｂ、ｂ、Ｔ、Ｔ 分别取 ０．５、０、６．０ｓ和 ０ｓ，计算结果如图 ２。
ｐ
ｔ
ｎ
ｄ
表 ２ 初始稳态时的机组参数
３
机组编号 出力?ＭＷ 工作水头?ｍ 引用流量?（ｍ ?ｓ） ｓ ｓ ｓ ３ ｓ
４
１
２
３ ＃ ３５７．１３ ４８０．９６ ８４．０４ － ０．６５３ ０．７４６ － １．９７３ ０．６６２
４ ＃ ３５７．１３ ４８０．９６ ８４．０４ － ０．６５３ ０．７４６ － １．９７３ ０．６６２
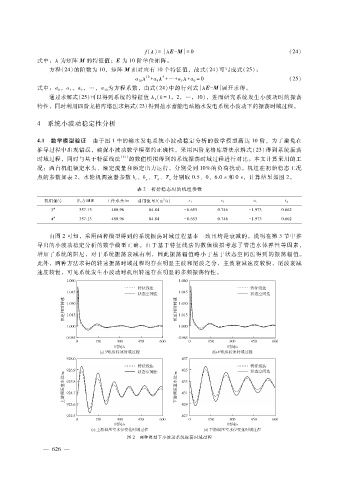
由图 ２可知，采用两种模型得到的系统振荡时域过程基本一致且均是衰减的，说明在第 ３节中推
导出的小波动稳定分析的数学模型正确。由于基于特征线法的数值模拟考虑了管道水体弹性等因素，
增加了系统的阻尼，对于系统振荡衰减有利，因此振荡幅值略小于基于状态空间法得到的振荡幅值。
此外，两种方法求得的转速振荡时域过程均存在明显主波和尾波之分，主波衰减速度较快，尾波衰减
速度较慢，可见系统发生小波动时机组转速存在明显的多频振荡特性。

图 ２ 两种模型下小波动系统振荡时域过程
— ６ ２ —
６