Page 73 - 2023年第54卷第6期

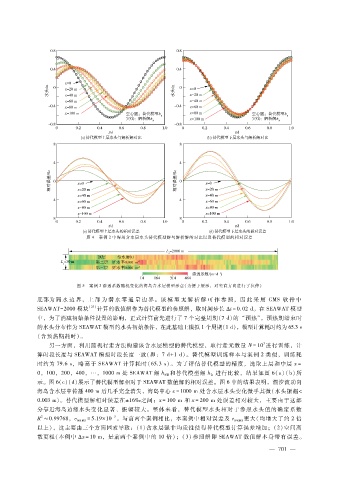
图 ４ 案例 ２中海岛含水层水头替代模型解与解析解的对比以及替代模型的相对误差

图 ５ 案例 ３渗透系数随机变化的海岛含水层模型示意（为便于展示，对竖直方向进行了拉伸）

底部为 隔 水 边 界， 上 部 为 潜 水 零 通 量 边 界。 该 模 型 无 解 析 解 可 作 参 照， 因 此 采 用 ＧＭＳ软 件 中
ＳＥＡＷＡＴ － ２０００模块 ［２７］ 计算的数值解作为替代模型的参照解，取时间步长 Δ ｔ ＝ ００２ｄ 。在 ＳＥＡＷＡＴ模型
中，为了消减初始条件设置的影响，正式计算前先进行了 ７个完整周期（７ｄ）的 “预热”。预热期结束时
的水头分布作为 ＳＥＡＷＡＴ模型的水头初始条件，在此基础上模拟 １个周期（１ｄ），模型计算耗时约为 ６５．３ｓ
（含预热期耗时）。
５
另一方面，利用随机行走方法构建该含水层模型的替代模型，取行走元数量 Ｎ＝ １０进行训练，计
算时段长度与 ＳＥＡＷＡＴ模拟时段长度一致（即：７ｄ ＋ １ｄ）。替代模型训练样本与案例 ２类似，训练耗
时约为 ７９．６ｓ，略高于 ＳＥＡＷＡＴ计算耗时（６５．３ｓ）。为了评估替代模型的精度，选取上层和中层 ｘ ＝
０ ，１００，２００，４００，…，１０００ｍ处 ＳＥＡＷＡＴ解 ｈ 和替代模型解 ｈ 进行比较，结果如图 ６（ａ）（ｂ）所
ＳＷ
Ｒ
示。图 ６（ｃ）（ｄ）展示了替代模型解相对于 ＳＥＡＷＡＴ数值解的相对误差。图 ６中的结果表明，潮汐波动向
海岛含水层中传播 ４００ｍ后几乎完全消失，海岛中心 ｘ ＝ １０００ｍ处含水层水头变化微乎其微（水头振幅＜
０．００３ｍ ）。替代模型解相对误差在±１６‰之间；ｘ ＝ １００ｍ 和 ｘ ＝ ２００ｍ处误差相对较大，主要由于这部
分靠近海岛边缘水头变化显著、振幅较大。整体来看，替代模型水头相对于参照水头值的确定系数
２
－ ３
Ｒ≈０．９９７６８，ｅ ＝ ５．１９ × １０ 。与前两个案例相比，本案例中相对误差及 ｅ 更大（均增大了约 ２倍
ＮＲＭＳ
ＮＲＭＳ
以上），这主要由三个方面因素导致：（ １）含水层强非均质性使得替代模型计算误差增加；（２）空间离
散更粗（本例中 Δ ｘ ＝ １０ｍ，是前两个案例中的 １０倍）；（３）参照解即 ＳＥＡＷＡＴ数值解本身带有误差。
— ７ ０ １ —