Page 57 - 2024年第55卷第1期

模型的前后处理分为多个步骤：（１）前处理过程中，先建立几何模型并划分网格，导出包含节点
信息的基础数据；（ ２）编写并执行 Ｐｙｔｈｏｎ脚本文件 １，基于试验布置选择钢丝断点的节点编号和节点坐
标；（ ３）在钢丝断点处添加新的钢丝节点，修改断点处的钢丝单元；（４）编写并执行 Ｐｙｔｈｏｎ脚本文件
２，匹配与钢丝节点重叠的混凝土节点和砂浆节点；（５）插入线性和非线性弹簧单元，以传递钢丝的预
压应力、模拟钢丝断裂和钢丝黏结滑移；（ ６）添加其它模型信息，主要包括材料属性、接触作用、边
界条件、初始温度场和荷载步等等；（ ７）编写 Ｐｙｔｈｏｎ脚本文件 ３，提取有限元结果文件中的断丝节点
位移、单元积分点坐标和钢丝单元的拉应力等计算结果。其中，断丝节点位移可用于计算钢丝断口开
度，并从侧面反映断丝预应力损失范围及其扩展规律；断丝拉应力变化能直接获得断丝预应力的损失
范围；单元积分点坐标可用于坐标转换，将圆柱面展开成平面以更好地展示计算结果。
３．２ 参数敏感性分析 采用控制变量法进行参数敏感性分析。若未额外说明，计算参数的默认值如下取
值：非线性弹簧单元的极限拉力（与网格尺寸有关）为 １４１１Ｎ；内聚力模型中，弹性模量均为 ２００ＭＰａ，
破坏时的有效位移为 １０ｍｍ；塑性损伤模型中，砂浆的本构关系取值依据 《混凝土结构设计规范》
（ ＧＢ５００１０—２０１０） ［２３］ （包含下降段参数为 １．９６），黏性系数为 ０．０５；每个断丝荷载步割断 １根钢丝。
其中，与标准取值存在差异的会单独说明原因。
预应力钢丝断裂后，断丝和薄层砂浆之间借助环向非线性弹簧单元形成断丝的黏结滑移。弹簧单
元的相对位移是两个节点的位移分量之间的差值。参考欧洲模式规范 ［２４］ ，单轴加载下混凝土和钢筋之
间的黏结应力是相对位移的函数
ｓ
( ) α ，０ ≤ｓ ≤ｓ
τ ｍａｘ １
ｓ
１
，ｓ ≤ｓ ≤ｓ
τ ｍａｘ １ ２
ｆ（ｓ） ＝ （１）
ｓ － ｓ
２
－ ） ，ｓ ≤ｓ ≤ｓ
τ ｍａｘ － （ τ ｍａｘ τ ｆ ２ ３
ｓ － ｓ
２
３
，ｓ ≤ｓ
τ ｆ ３
为黏结强度特征值；ｓ、ｓ和 ｓ为滑移特征值。对于黏结条件良好的光圆钢筋，黏结强
式中：τ ｍａｘ 和 τ ｆ １ ２ ３
度与抗压强度标准值 槡 ｃｋ ＝ ＝ ０ ．１ ｆ；指数项简化为 α ＝ １ ；滑移特征值参考冷拉钢丝
槡
ｆ有关，即 τ ｍａｘ τ ｆ
ｃｋ
的取值，即 ｓ＝ ｓ＝ ｓ＝ ０．０１ｍｍ 。
１
２
３
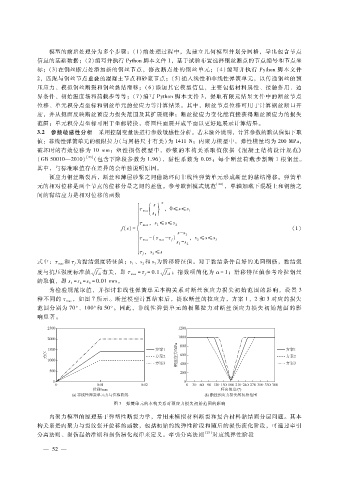
为检验规范取值，并探讨非线性弹簧单元本构关系对断丝预应力损失初始范围的影响，设置 ３
，如图 ７所示。断丝模型计算结束后，提取断丝的拉应力，方案 １、２和 ３对应的损失
种不同的 τ ｍａｘ
范围分别为 ７０°、１００°和 ５０°。因此，非线性弹簧单元的极限拉力对断 丝预 应 力 损失 初 始 范围的 影
响显著。

图 ７ 弹簧单元的本构关系对预应力损失初始范围的影响

内聚力模型的原理基于弹塑性断裂力学，常用来模拟材料断裂和复合材料黏结面分层问题。其本
构关系是内聚力与裂纹张开位移的函数，包括初始的线弹性阶段和随后的损伤演化阶段，可通过牵引
分离法则、损伤起始准则和损伤演化规律来定义。牵引分离法则 ［２５］ 对应线弹性阶段

— ５ ２ —