Page 62 - 2024年第55卷第1期
P. 62
4.3 模拟应变的验证 以管芯内表面为例,验证模型参数选取的合理性,并说明预应力损失的扩展过
程,如图 14所示。为了与试验数据比对,提取有限元模型的环向应变,并将预应力施加结束时的应
- 6
变定义为初始的零应变。当内水压力加载至 1.15MPa时,测试与模拟环向应变均约为 200 × 10 ,并
表明数值模型在弹性阶段的参数取值合理。断丝数量不超过 40根时,测试与模拟结果均在靠近断丝
区处应变增大,远离断丝区处变形不变,并表明数值模型能展现管芯预应力的损失区间。在未开裂
- 6
- 6
前,测试应变低于 400 × 10 ,模拟应变在未发生突变前同样在低于 400 × 10 。管芯开裂后,测试应变
和模拟应变都发生突变,形成多个应变尖峰,且峰值的相对值大小相差不多。图 14(a)(b)的对比表
明模拟结果在断点处的应力集中,因而过早发生应变凸起;试验结果中管芯预应力损失具有突发性。
图 14(c)(d)的对比表明,受砂浆黏度系数 μ取值为 0.05的影响,模拟结果预应力损失在环向上的扩
展速度较慢;模拟应变与测试应变在数量级上一致。
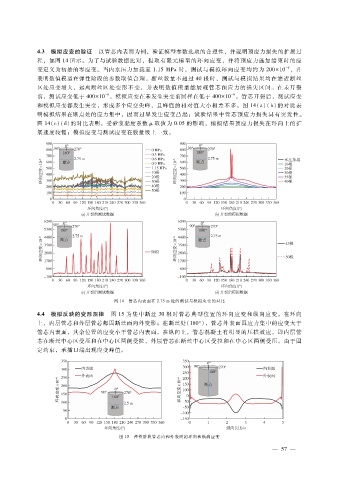
图 14 管芯内表面在 2.75m处的测试与模拟应变的对比
4.4 模拟反映的变形规律 图 15为集中断丝 30根时管芯典型位置的环向应变和纵向应变。在环向
上,内层管芯和外层管芯都因断丝而向外变形;在断丝处(180°),管芯外表面因应力集中的应变大于
管芯内表面,其余位置的应变小于管芯内表面。在纵向上,管芯混凝土有明显的压拱效应,即内层管
芯在断丝中心区受压和在中心区两侧受拉,外层管芯在断丝中心区受拉和在中心区两侧受压。由于固
定约束,承插口端出现应变峰值。
图 15 弹性阶段管芯内和外表面的环向和纵向应变
— 5 7 —