Page 59 - 2024年第55卷第1期

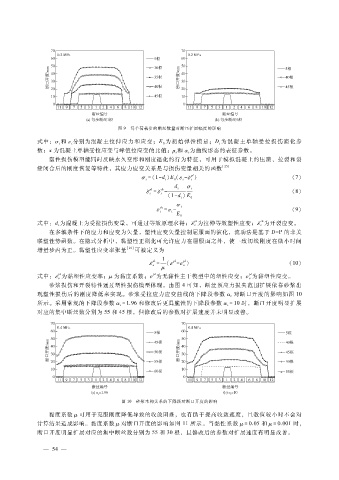
图 ９ 每个荷载步的断丝数量对断口扩展幅度的影响
分别为混凝土拉伸应力和应变；Ｅ 为初始弹性模量；Ｄ为混凝土单轴受拉损伤演化参
式中：σ ｔ 和 ε ｔ ０ ｔ
为曲线形态的表征参数。
数；ｘ为混凝土单轴受拉应变与峰值拉应变的比值；ρ ｔ 和 α ｔ
塑性损伤模型能同时反映永久变形和刚度退化的行为特征，可用于模拟混凝土的压溃、拉裂和裂
缝闭合后的刚度恢复等特性，其应力应变关系是与损伤变量相关的函数 ［２５］
ｐｌ
－ ε ） （７）
σ ｔ ＝ （１ － ｄ）Ｅ（ ε ｔ 珘 ｔ
ｔ
０
ｄ ｔ σ ｔ
ｃｋ
ｐｌ
ε ＝ ε － （８）
珘 ｔ 珘 ｔ
（１ － ｄ）Ｅ ０
ｔ
σ ｔ
ｃｋ
ε ＝ － （９）
珘 ｔ ε ｔ
Ｅ
０
ｐｌ ｃｋ
ｔ
式中：ｄ为混凝土为受拉损伤变量，可通过等效原理求得； 珘 ｔ ε 为开裂应变。
ε 为拉伸等效塑性应变； 珘 ｔ
在多轴条件下的应力和应变为矢量，塑性应变矢量控制屈服面的演化，流动法是基于 Ｄ － Ｐ的非关
联塑性势函数。在隐式分析中，黏塑性正则化可允许应力在屈服面之外，使一致切线刚度在微小时间
增量步内为正。黏塑性应变率张量 ［２５］ 可被定义为
１
ｐｌ ｐｌ ｐｌ
＝ （ ε － ε ｖ
ε ｖ ） （１０）
μ
ｐｌ ｐｌ ｐｌ
ε ｖ
式中： 为黏塑性应变率；μ为黏度系数；ε 为无黏性主干模型中的塑性应变；ε ｖ 为黏塑性应变。
砂浆损伤和开裂特性通过塑性损伤模型体现。由图 ４可知，断丝预应力损失范围扩展依靠砂浆出
对断口开度的影响如图 １０
现塑性损伤后的刚度降低来实现。砂浆受拉应力应变曲线的下降段参数 α ｔ
＝ １０时，断口开度明显扩展
所示。采用常规的下降段参数 α ｔ ＝ １．９６和修改后更具脆性的下降段参数 α ｔ
对应的集中断丝数分别为 ５５和 ４５根，但修改后的参数对扩展速度并未明显改善。

图 １０ 砂浆本构关系的下降段对断口开度的影响
黏度系数 μ可用于克服刚度降低导致的收敛困难，也有助于提高收敛速度，且数值较小时不会对
计算结果造成影响。黏度系数 μ对断口开度的影响如图 １１所示。当黏性系数 μ ＝ ０ ．０５和 μ ＝ ０ ．００１时，
断口开度明显扩展对应的集中断丝数分别为 ５５和 ３０根，且修改后的参数对扩展速度有明显改善。

— ５ ４ —