Page 11 - 2024年第55卷第7期

５ 预测结果及分析

５．１ 模型预测结果 模型首先采用 ２０１７年 ９月 ４日—２０２０年 １１月 ２３日所有的微震数据对模型进行
检验，由于模型抽取相同数量的发生岩爆及未发生岩爆的样本，样本中仍有 １０３４４个发生岩爆样本未
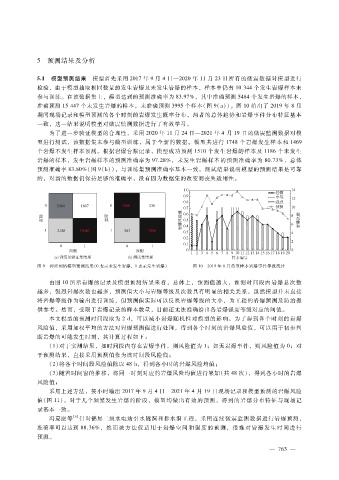
参与训练。在该数据集上，模型达到的预测准确率为 ８３．９７％，其中准确预测 ５４８４个发生岩爆的样本，
准确预测 １５４４７个未发生岩爆的样本，未准确预测 ３９９５个样本（图 ９（ａ））。图 １０给出了 ２０１９年 ８月
期间现场记录和模型预测的各个时刻的岩爆发生概率分布，两者的总体趋势和岩爆事件分布特征基本
一致，这一结果说明模型对微震监测数据进行了有效学习。
为了进一步验证模型的合理性，采用 ２０２０年 １１月 ２４日—２０２１年 ４月 １９日的微震监测数据对模
型进行测试，该数据集未参与模型训练，属于全新的数据。模型共进行 １７４８个岩爆发生样本和 １４６９
个岩爆不发生样本预测。根据岩爆台账记录，模型成功预测 １５１０个发生岩爆的样本及 １１８６个未发生
岩爆的样本，发生岩爆样本的预测准确率为 ９７．２８％，未发生岩爆样本的预测准确率为 ８０．７３％，总体
预测准确率 ８３．８０％（图 ９（ｂ）），与训练集预测准确率基本一致。测试结果说明模型的预测结果是可靠
的，对新的数据仍保持足够的准确率，没有因为数据集的改变而丧失适用性。

图 ９ 神经网络模型预测结果（０表示未发生岩爆，１表示发生岩爆） 图 １０ ２０１９年 ８月典型样本岩爆事件等级统计

由图 １０所示岩爆的记录及模型预测结果来看，总体上，预测值越大，预测时间段内岩爆总次数
越多，强烈岩爆次数也越多，预测值大小与岩爆等级及次数具有明显的相关关系。虽然模型并未直接
将岩爆等级作为输出进行训练，但预测值实际可以反映岩爆等级的大小，为工程的岩爆预测及防治提
供参考。然而，受限于岩爆记录的样本数量，目前还无法准确给出各岩爆强度等级对应的阈值。
本文模型的预测时间段取为 ２ｄ，可以减小岩爆随机性对模型的影响。为了得到各个时刻的岩爆
风险值，采用加权平均的方法对岩爆预测值进行处理，得到各个时刻的岩爆风险值，可以用于初步判
断岩爆的可能发生时刻，其计算过程如下：
（ １）对于实测结果，如时间段内存在岩爆事件，则风险值为 １；如无岩爆事件，则风险值为 ０；对
于预测结果，直接采用预测值作为该时间段风险值；
（２）将各个时间段风险值除以 ４８ｈ，得到各小时的岩爆风险均值；
（ ３）随着时间窗的推移，将同一时刻对应的岩爆风险均值进行累加（共 ４８次），得到各小时的岩爆
风险值；
采用上述方法，按小时输出 ２０１７年 ９月 ４日—２０２１年 ４月 １９日现场记录和模型预测的岩爆风险
值（图 １１），对于几个频繁发生岩爆的阶段，模型均做出有效的预测，得到的岩爆分布特征与现场记
录基本一致。
冯夏庭等 ［６］ 针对锦屏二级水电站引水隧洞和排水洞工程，采用连续微震监测数据进行岩爆预测，
准确率可以达到 ８８．３６％，然而该方法仅适用于岩爆空 间和 强度 的预 测，很 难对 岩爆 发生 时 间进行
预测。

— ７ ６ ３ —