Page 23 - 2024年第55卷第7期
P. 23
不足影响、调峰水量充裕。
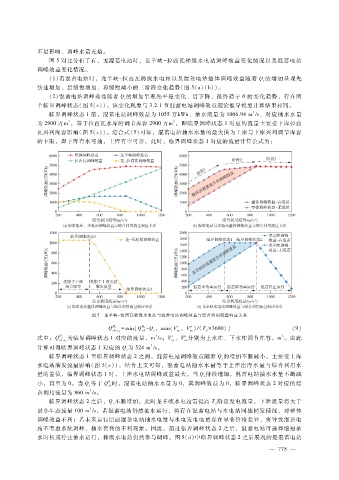
图 5对比分析了有、无混蓄电站时,龙羊峡 - 拉西瓦梯级水电站调峰效益变化情况以及混蓄电站
调峰效益变化情况。
(1)有混蓄电站时,龙羊峡- 拉西瓦梯级水电站以及混蓄电站整体调峰效益随着 Q的增加呈现先
s
快速增加、后缓慢增加、再缓慢减小的三阶段变化趋势(图 5(a)(b))。
( 2)混蓄电站调峰效益随着 Q的增加呈现先平稳变化、后下降、最终趋于 0的变化趋势,存在两
s
个临界调峰状态(图 5(c))。该变化现象与 3.2.1节混蓄电站调峰效益理论推导模型计算结果相同。
3
临界调峰状态 1前,混蓄电站调峰效益为 1055万kWh、抽水流量为 1006.94m ?s、对应抽水水量
3
3
为 2900万m ,等于拉西瓦水库的调节库容 2900万m ,即临界调峰状态 1对应的流量主要受下库拉西
瓦兴利库容影响(图 5(c))。结合式(5)可知,混蓄电站抽水水量的最大值为上库与下库兴利调节库容
的下限,即下库有水可抽,上库有空可蓄。此时,临界调峰状态 1对应的流量计算公式为:
图 5 龙羊峡- 拉西瓦梯级水电站与混蓄电站调峰效益与综合利用流量响应关系
H i
Q H i = min[Q - Q,min(V′,V″)?(T× 3600)] (9)
cd,s 1 cd s uc uc 2
3
3
式中:Q H i 为临界调峰状态 1对应的流量,m ?s;V′、V″分别为上水库、下水库调节库容,m 。由此
cd,s 1 uc uc
3
计算可得临界调峰状态 1对应的 Q为 524m ?s。
s
临界调峰状态 1至临界调峰状态 2之间,混蓄电站调峰效益随着 Q的增加不断减小,主要受上库
s
水电站满发流量影响(图 5(c))。结合上文可知,混蓄电站抽水水量等于上库出库水量与综合利用水
量的差值,临界调峰状态 1时,上库水电站调峰效益最大。当 Q持续增加,混蓄电站抽水水量不断减
s
小,直至为 0。当 Q等于 Q 时,混蓄电站抽水水量为 0,其调峰效益为 0,临界调峰状态 2对应的综
R i
s cd
3
合利用流量为 860m ?s。
临界调峰状态 2之后,Q不断增加,此时龙羊峡水电站需提高 T阶段发电流量,下泄流量将大于
2
s
3
最小生态流量 100m ?s。若混蓄电站仍然抽水运行,将存在混蓄电站与水电站同抽同发情况,对整体
调峰效益不利;若未来运行层面混蓄电站抽水电量与水电发电电量存在显著价格差异,将导致混蓄电
站不考虑系统调峰、抽水套利的不利现象。因此,超过临界调峰状态 2之后,混蓄电站可选择缩短抽
水时长或停止抽水运行,梯级水电站仍然参与调峰。图 5(d)中临界调峰状态 2之后展现的是混蓄电站
— 7 7 5 —