Page 68 - 2024年第55卷第7期

３ （１ － Ｋ ）（２ ＋ Ｋ ） Ｍ ２
Ｔ
０Ｔ
０Ｔ
＝ － （５）
α Ｔ ２
（１ ＋ ２Ｋ ） ３
０Ｔ
式中：Ｋ 为土在某一温度下的 Ｋ系数；Ｍ 为土在某一温度下的临界状态应力比。Ｙａｏ等 ［２６］ 以及 Ｋｏｎｇ
０Ｔ ０ Ｔ
等 ［２１］ 认为升温使得正常固结土体积收缩、密度增大，土的强度随之提高，并采用下式计算 Ｍ ：
Ｔ
－
[ λ Ｔ κ Ｔ ]
Ｍ ＝ （Ｍ－ Ｍ ）ｅｘｐ λ － κ （Ｔ － Ｔ） ＋ Ｍ ｈ （６）
Ｔ
ｈ
０
为土
ｈ
式中：Ｍ 为 Ｈｖｏｒｓｌｅｖ线斜率；λ为土的压缩指数；κ为土的回弹指数；λ Ｔ 为土的热压缩指数；κ Ｔ
的热回弹指数。
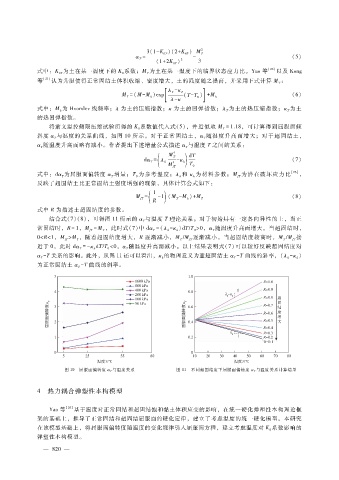
将前文温控侧限压缩试验所得的 Ｋ系数值代入式（５），并近似取 Ｍ ＝ １．１８，可计算得到屈服面倾
Ｔ
０
随温度升高而增大；对于超固结土，
斜度 α Ｔ 与温度的关系曲线，如图 １０所示。对于正常固结土，α Ｔ
与温度 Ｔ之间的关系：
α Ｔ 随温度升高而略有减小。作者提出下述增量公式描述 α Ｔ
( Ｍ ４ ｄＴ
Ｔ
－ κ ｋ
ｄ α Ｔ ＝ λ ｋ ４ ) Ｔ （７）
Ｍ
ｆＴ ０
为材料参数；Ｍ 为潜在破坏应力比 ［２６］ ，
０ ｆＴ
式中：ｄ α Ｔ 为屈服面偏转度 α Ｔ 增量；Ｔ为参考温度；λ ｋ 和 κ ｋ
反映了超固结土比正常固结土强度增强的现象，具体计算公式如下：
１
Ｍ ＝ ( ) （８）
－ １ （Ｍ － Ｍ ） ＋ Ｍ
ｆＴ Ｒ Ｔ ｈ Ｔ
式中 Ｒ为描述土超固结度的参数。
与温度 Ｔ理论关系。对于初始具有一定各向异性的土，当正
结合式（ ７）（８），可得图 １１所示的 α Ｔ
随温度升高而增大。当超固结时，
常固结时，Ｒ ＝ １，Ｍ ＝ Ｍ ，此时式（７）中 ｄ α Ｔ ＝ （ λ ｋ κ ｋ ０
ｆＴ
－ ）ｄＴ?Ｔ＞０，α Ｔ
Ｔ
０＜Ｒ＜１，Ｍ ＞Ｍ ，随着超固结度增大，Ｒ逐渐减小，Ｍ ?Ｍ 逐渐减小。当超固结度较高时，Ｍ ?Ｍ 接
Ｔ
ｆＴ
Ｔ
ｆＴ
ｆＴ
Ｔ
随温度升高而减小。以上结果表明式（７）可以较好反映超固结度对
近于 ０，此时 ｄ α Ｔ ＝－ κ ｋ ｄＴ?Ｔ＜０，α Ｔ
０
－ ）
α Ｔ － Ｔ关系的影响。此外，从图 １１还可以看出，κ ｋ 的物理意义为重超固结土 α Ｔ － Ｔ曲线的斜率，（ λ ｋ κ ｋ
－ Ｔ曲线的斜率。
为正常固结土 α Ｔ

图 １０ 屈服面偏转度 α Ｔ 与温度关系 图 １１ 不同超固结度下屈服面偏转度 α Ｔ 与温度关系计算结果

４ 热力耦合弹塑性本构模型

Ｙａｏ等 ［２６］ 基于温度对正常固结和超固结饱和黏土体积应变的影响，在统一硬化弹塑性本构理论框
架的基础上，推导了正常固结和超固结屈服面的硬化定律，建立了考虑温度的统一硬化模型。本研究
在该模型基础上，将屈服面偏转度随温度的变化规律引入屈服面方程，建立考虑温度对 Ｋ系数影响的
０
弹塑性本构模型。

０
— ８ ２ —