Page 94 - 2024年第55卷第8期

的输入数据维度为 ４ × ３ × Ｔ。例如，当前时刻为 ｔ时，选取［ｔ － Ｔ，ｔ］的坝体地震响应信号作为模型输入
数据；取［ ｔ，ｔ ＋ Ｔ］的自由场地震时程作为检验模型预测值的真实样本。考虑到实际算力、时效性和精
度之间的平衡，Ｔ和 Δ ｔ分别取 ２０００和 ５，即时间窗长度为 １０ｓ，滑动间隔为 ０．０２５ｓ。故总共划分了
５３４组数据样本，每一组数据样本中均包含 ４个坝体测点和 １个坝区自由场测点的 ３个方向地震数据，
即数据样本维度为 ５３４ × ５ × ３ × ２０００。随机选取其中 ８０％作为训练集，２０％作为测试集，分别用于模型
参数训练和性能评估。ＴＦＡ － Ｓｅｑ２Ｓｅｑ模型的隐藏层数和每个隐藏神经元数量分别设置为 ６４和 ３２，强
－ ４
制学习概率为 ０．５，学习率为 １ × １０ ，并设置学习率按指数衰减以提高模型收敛性。
２
通过对测试集的输出结果进行分析，得出虚拟传感器的 ＭＳＥ和 Ｒ 分别为 ０．０１１２和 ０．９６５４，取其
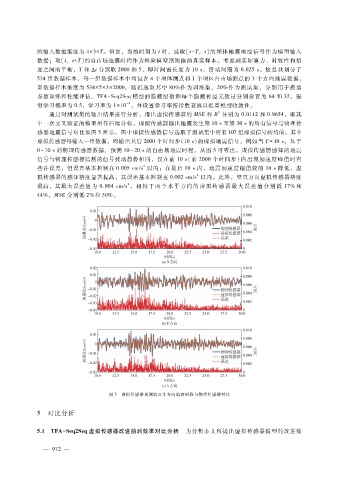
中一次交叉验证的模型用作后续分析。虚拟传感器输出地震发生第 １０ｓ至第 ３０ｓ的所有信号与物理传
感器地震信号对比如图 ５所示，图中虚拟传感器信号选取了测试集中所有 １０７组虚拟信号的均值。其中
虚拟传感器每输入一组数据，均输出其后 ２０００个时间步（１０ｓ）的虚拟地震信号，例如当 Ｔ ＝ １０ｓ ，基于
０～１０ｓ的物理传感器数据，预测 １０～２０ｓ的自由场地震时程。从图 ５可看出，虚拟传感器感知的地震
信号与物理传感器监测的信号波动趋势相同，仅在前 １０ｓ（前 ２０００个时间步）内出现加速度峰值时有
２
些许误差，但误差基本控制在 ０．００５ｃｍ?ｓ以内；在最后 １０ｓ内，地震加速度幅值较前 １０ｓ降低，虚
２
拟传感器的感知精度显著提高，其误差基本控制在 ０．００２ｃｍ?ｓ以内。此外，竖直方向虚拟传感器精度
２
最高，其最大误差值 为 ０．００４ｃｍ?ｓ，相较于两 个水平方 向的 虚拟 传 感 器 最 大 误 差 值 分 别 低 １７％和
４４％，ＭＳＥ分别低 ２％和 ３０％。

图 ５ 虚拟传感器预测的三个方向地震时程与物理传感器对比

５ 对比分析

５．１ ＴＦＡ － Ｓｅｑ２Ｓｅｑ虚拟传感器改进前后效果对比分析 为分析本文所提出虚拟传感器模型的改进效

— ９ ７ —
２