Page 48 - 2024年第55卷第9期

从表 ２可看出，本文方法降噪误差比最高，相较其他模型 表 ２ 大坝变形序列降噪效果评价指标
分别改善了 ５．６６％、３０．１０％、１９．５４％、４１．５５％。从图 ４可看出， 方法 含噪信号降噪误差比
变形数据序列整体受噪声影响存在明显 “突刺”，经过所提降噪 ＥＥＭＤ ４３．８８９８
方法处理之后，“突刺” 信号与大部分的小幅度波动均被有效剔 ＴＥＥＭＤ ５１．９６９９
除，原始变形数据序列变得更加平滑；在水位等环境量发生波
ＧＷＯ － ＣＥＥＭＤＡＮ ４７．７５４０
动而导致 位 移 出 现较大 拐点 处，拐 点有 效 信息也 未发 生 失 真，
ＴＣＥＥＭＤＡＮ ５８．７９９８
可有效提取出真实信号特征。
Ｐｒｏｐｏｓｅｄ ６２．１２５９
３．３ 最优特征集合筛选 针对已降噪位移数据与特征集合，采
用 ２．２节所述方法筛选最优因子集。由于 ＲＦＥＣＶ的稳定性与选用的学习器具有相关性，最佳特征组合
可能随着元学习器的改变而改变。因此本文选取三种广泛使用且效果较好的回归方法作为学习器，分
别为多元线性回归（ＭｕｌｔｉｐｌｅＬｉｎｅａｒＲｅｇｒｅｓｓｉｏｎ，ＭＬＲ）、Ｎｕ － 支持向量回归（Ｎｕ － ＳｕｐｐｏｒｔＶｅｃｔｏｒＲｅｇｒｅｓｓｉｏｎ，
ＮｕＳＶＲ）与岭回归（ＲｉｄｇｅＲｅｇｒｅｓｓｉｏｎ，ＲＲ），对所有可能的特征数量及相应特征集合进行遍历。同时对
于 ｋ折交叉试验来说，随着 ｋ取值的不同，试验结果也会有所不同，考虑拟合的良好性 ［２６］ ，本文分别
２
以 ５、８、１０折交叉试验所得决定系数 Ｒ的均值作为评价指标来选取最优学习器与最优特征集合。
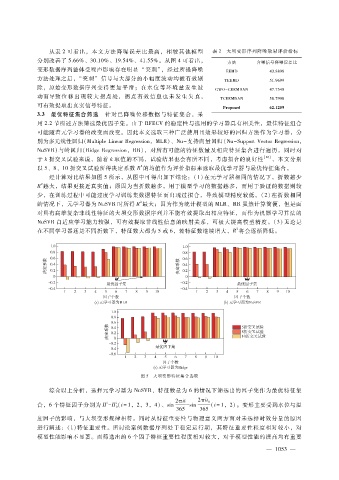
经计算对比结果如图 ５所示，从图中可得出如下结论：（１）在元学习器相同的情况下，折数越少
２
Ｒ越大，结果更接近真实值；原因为当折数越多，用于模型学习的数据越多，而用于验证的数据则较
少，在训练过程中可能过度学习训练集数据特征而出现过拟合，导致模型精度较低。（２）在折数相同
２
的情况下，元学习器为 ＮｕＳＶＲ时所得 Ｒ最大；因为作为统计模型的 ＭＬＲ、ＲＲ虽然计算简便，但是面
对具有高维复杂非线性特征的大坝变形数据序列并不能有效提取出相应特征，而作为机器学习算法的
ＮｕＳＶＲ自适应学习能力较强，可有效提取非线性信息的映射关系，可极大提高模型精度。（３）无论是
２
在不同学习器还是不同折数下，特征数大都为 ５或 ６，若特征数继续增大，Ｒ将会逐渐降低。

图 ５ 大坝变形特征集合选取

综合以上分析，选择元学习器为 ＮｕＳＶＲ、特征数量为 ６的情况下筛选出的因子集作为最优特征集
２ π ｉｔ ２ π ｉｔ
０
ｉ
ｉ
合，６个特征因子分别为 Ｈ－ Ｈ（ｉ ＝ １ ，２，３，４）、ｓｉｎ － ｓｉｎ （ｉ ＝ １ ，２）。变形主要受到水位与温
０
３６５ ３６５
度因子的影响，与大坝变形规律相符。同时从特征重要性与物理意义两方面对未选择时效分量的原因
进行阐述：（ １）特征重要性。所讨论案例数据序列处于稳定运行期，其特征重要性程度相对较小，对
模型性能影响不显著。而筛选出的 ６个因子特征重要性程度相对较大，对于模型性能的提高均有重要
０
— １ ５ ３ —