Page 47 - 2024年第55卷第9期

其余为测试集。
３．１ 特征因子构建 结合大坝特性及参考文献，环境温度会对大坝变形产生周期性影响，则添加参数
的谐波函数表示温度因子；时效因子表示坝体材料劣化程度，降低坝体力学性能；而静水位等环境量
会引起坝体可逆变形；因此以温度、时效与水压分量为特征因子构建因子分析模型进行变形预测，见
式（ １５）：
＋δ
δ ＝δ Ｈ ＋δ Ｔ
θ
４
ｉ
ｉ
＝
δ Ｈ ∑ ａ（Ｈ －Ｈ）
０
ｉ
ｉ ＝１
２ ２ π ｉｔ ２ ２ π ｉｔ （１５）
( [
∑
δ Ｔ ∑ ｂ ｓｉｎ ２ π ｉｔ －ｓｉｎ ０ )] [ ２ｉ ( ２ π ｉｔ －ｃｏｓ ０ )]
＝
＋
ｂ ｃｏｓ
１ｉ
ｉ ＝１ ３６５ ３６５ ｉ ＝１ ３６５ ３６５
）
２
１
δ ＝ｃ（ θ－θ ０ ）＋ｃ（ｌｎ θ－ｌｎ θ ０
θ
＝ｔ ?１００
θ ＝ｔ ?１００，θ ０ ０
、δ为相应水压、温度与时效分量；Ｈ、Ｈ分别为监测日、始测日上游
式中：δ 为坝体变形值；δ Ｈ 、δ Ｔ
θ ０
相应水位；ｔ、ｔ分别为监测日、序列第一日至始测日 累计 天 数；ａ、ｂ、ｂ、ｃ、ｃ 为各 分 量回归
０ ｉ １ｉ ２ｉ １ ２
系数。
对时序数据进行归一化消除变量间的量纲差异，见式（１６）：
ｘ － ｘ
Ｍ ＝ ｉ ｍｉｎ （１６）
ｉ
ｘ － ｘ
ｍａｘ ｍｉｎ
式中：ｘ为初始数据；Ｍ 为计算结果；ｘ 、ｘ 分别为初始数据中的最大值与最小值。
ｉ ｉ ｍａｘ ｍｉｎ
３．２ 变形序列分解与降噪 采用 ２．１节所述方法对所选测点历史变形数据进行降噪重构。由于 ＣＥＥＭ
ＤＡＮ参数中的分解层数 ｍａｘ＿ｉｍｆ、添加次数 ｔｒｉａｌｓ及噪声幅值 ｅｐｓｉｌｏｎ对信号分解效果具有较大影响，
故采用 ２．１．３节 ＧＷＯ对上述三个参数组合开展寻优，设置狼群个体为 ２０头，迭代次数为 １００轮。其
中 ｍａｘ＿ｉｍｆ寻优范围为［３，８］，ｔｒｉａｌｓ寻优范围为［６０，２７０］，ｅｐｓｉｌｏｎ的寻优范围为［０．０１，１］，其余参
数均选取默认值；参数寻优结束后可输出最佳位置信息，即最优参数组合为［ ３，２１１，０．０２］。在该参
数组合下采用 ２．１．１节 ＣＥＥＭＤＡＮ法对原始数据序列进行分解，可得 ４个 ＩＭＦ分量与 １个残余分量，由
皮尔逊相关系数法可确定前三个分量相关系数均较小且相关性为 “极弱相关”，而 ＩＭＦ与 ＩＭＦ相关系数
３ ４
相差较大且相关性所处区间间隔为 ４，符合 “突然增大”，故由相关系数原理可得 ＩＭＦ、ＩＭＦ、ＩＭＦ为
１
３
２
主要包含噪声的分量。按照 ２．１．３节的方法进行阈值降噪并重构，可得降噪信噪比为 ６２．１２５９。为验证
本文所提方法 （简称 Ｐｒｏｐｏｓｅｄ）的有效性，与 ＥＥＭＤ降噪法（简称 ＥＥＭＤ）、ＥＥＭＤ阈值 降噪 法 （简称
ＴＥＥＭＤ）、灰狼优化分解降噪法（简称 ＧＷＯ － ＣＥＥＭＤＡＮ）、ＣＥＥＭＤＡＮ阈值降噪法（简称 ＴＣＥＥＭＤＡＮ）
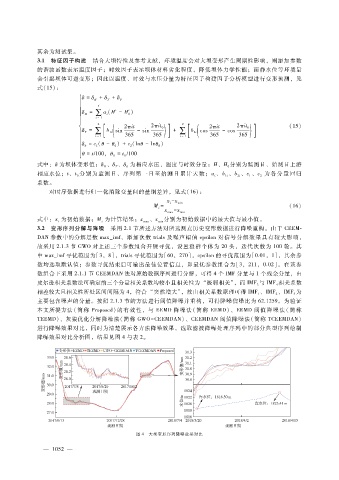
进行降噪效果对比，同时为清楚展示各方法降噪效果，选取滤波降噪处理序列中的部分典型序列绘制
降噪效果对比分析图，结果见图 ４与表 ２。

图 ４ 大坝变形序列降噪效果对比

— １ ０ ２ —
５