Page 112 - 2024年第55卷第12期

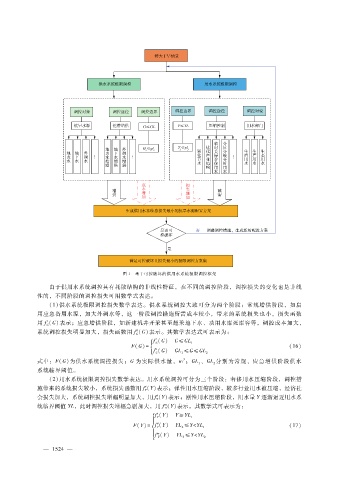
图 １ 基于可控破坏的供用水系统极限调控框架
由于供用水系统调控具有耗散结构的非线性特征，在不同的调控阶段，调控损失的变化也是非线
性的，不同阶段的调控损失可用数学式表达。
（ １）供水系统极限调控损失数学表达。供水系统调控大致可分为两个阶段：常规增供阶段，如启
用应急备用水源，加大外调水等，这一阶段调控措施所需成本较小，带来的系统损失也小，损失函数
用 ｆ′（Ｇ）表示；应急增供阶段，如新建机井开采甚至超采地下水、动用水库死库容等，调控成本加大，
Ｇ
系统调控损失明显加大，损失函数用 ｆ″（Ｇ）表示。其数学表达式可表示为：
Ｇ
{ ｆ′（Ｇ） Ｇ ≤ＧＬ １
Ｇ
Ｆ（Ｇ） ＝ ｆ″（Ｇ） ＧＬ≤Ｇ ≤ＧＬ ２ （１６）
１
Ｇ
３
式中：Ｆ（Ｇ）为供水系统调控损失；Ｇ为实际供水量，ｍ ；ＧＬ、ＧＬ分别为常规、应急增供阶段供水
１ ２
系统临界阈值。
（２）用水系统极限调控损失数学表达。用水系统调控可分为三个阶段：奢侈用水压缩阶段，调控措
施带来的系统损失较小，系统损失函数用 ｆ′（Ｙ）表示；弹性用水压缩阶段，较多行业用水被压缩，经济社
Ｙ
会损失加大，系统调控损失增幅明显加大，用 ｆ″（Ｙ）表示；刚性用水压缩阶段，用水量 Ｙ逐渐逼近用水系
Ｙ
统临界阈值 ＹＬ，此时调控损失增幅急剧加大，用 ｆ  （Ｙ）表示。其数学式可表示为：
Ｙ
ｆ′（Ｙ） Ｙ ≥ＹＬ
{ Ｙ １
Ｆ（Ｙ） ＝ ｆ″（Ｙ） ＹＬ≤Ｙ＜ＹＬ １ （１７）
Ｙ
２
ｆ  （Ｙ） ＹＬ≤Ｙ＜ＹＬ ２
３
Ｙ
— １ ５ ４ —
２