Page 130 - 2024年第55卷第12期

２
为均值 ０、方差 σ 的白噪声。在同时考虑
式中：ｃ为常数；ｐ为自回归模型的阶数；φ ｉ 为模型参数；ε ｔ
模型拟合优度和复杂度的情况下，最优阶数 ｐ由贝叶斯信息准则（ＢａｙｅｓｉａｎＩｎｆｏｒｍａｔｉｏｎＣｒｉｔｅｒｉｏｎ，ＢＩＣ）
确定，具体原理见文献［ ２８］。
经误差校正后的预报径流为：
Ｑ′ ＝ Ｑ － Ｘ （３）
ｓｉｍ，ｔ ｓｉｍ，ｔ ｔ
式中 Ｑ′ 为误差校正后的预报径流。
ｓｉｍ，ｔ
本文分别对候、旬、月尺度的平均模拟径流进行校正和预报，即得到未来 ５、１０和 ３０ｄ的平均预
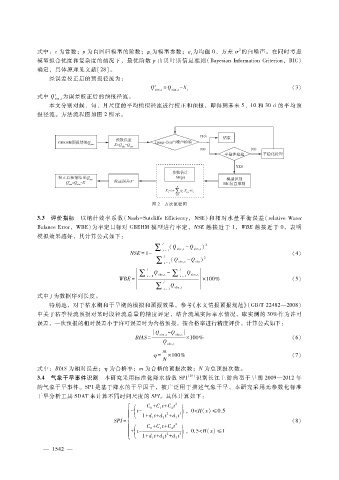
报径流。方法流程图如图 ２所示。

图 ２ 方法流程图

３．３ 评价指标 以纳什效率系数（Ｎａｓｈ － ＳｕｔｃｌｉｆｆｅＥｆｆｉｃｉｅｎｃｙ，ＮＳＥ）和相对水量平衡误差（ｒｅｌａｔｉｖｅＷａｔｅｒ
ＢａｌａｎｃｅＥｒｒｏｒ ，ＷＢＥ）为率定目标对 ＧＢＥＨＭ模型进行率定，ＮＳＥ越接近于 １，ＷＢＥ越接近于 ０，表明
模拟效果越好，其计算公式如下：
ｊ ２
（Ｑ － Ｑ ）
ｔ
∑ ＝１ ｏｂｓ，ｔ ｓｉｍ，ｔ
ＮＳＥ ＝ １ － （４）
ｊ ２
（Ｑ － 珚 Ｑ ）
ｔ
∑ ＝１ ｏｂｓ，ｔ ｏｂｓ
ｊ ｊ
Ｑ － Ｑ
∑ ＝１ ｏｂｓ，ｔ ∑ ＝１ ｓｉｍ，ｔ
ｔ
ｔ
ＷＢＥ ＝ × １００ ％ （５）
ｊ
Ｑ
ｔ
∑ ＝１ ｏｂｓ，ｔ
式中 ｊ为数据序列长度。
特别地，对于枯水期和干旱期的模拟和预报效果，参考《水文情报预报规范》（ＧＢ?Ｔ２２４８２—２００８）
中关于枯季径流预报对某时段径流总量的精度评定，结合流域实际来水情况，取实测的 ３０％作为许可
误差，一次预报的相对误差小于许可误差时为合格预报，按合格率进行精度评价。计算公式如下：
Ｑ ｓｉｍ，ｔ － Ｑ ｏｂｓ，ｔ
ＢＩＡＳ ＝ × １００ ％ （６）
Ｑ
ｏｂｓ，ｔ
ｍ
η ＝ × １００％ （７）
Ｎ
式中：ＢＩＡＳ为相对误差；η为合格率；ｍ为合格的预报次数；Ｎ为总预报次数。
［２９］
３．４ 气象干旱事件识别 本研究采用标准化降水指数 ＳＰＩ 识别长江上游典型干旱期 ２００９—２０１２年
的气象干旱事件。ＳＰＩ是基于降水的干旱因子，被广泛用于描述气象干旱，本研究采用无参数化标准
干旱分析工具 ＳＤＡＴ来计算不同时间尺度的 ＳＰＩ。具体计算如下：
２
( Ｃ＋ Ｃｔ ＋ Ｃｔ ３)
２
１
０
－ ｔ － ２ ，０＜Ｈ（ｘ） ≤０．５
３
１
２
ＳＰＩ ＝ １ ＋ ｄｔ ＋ ｄｔ ＋ ｄｔ （８）
２
( Ｃ＋ Ｃｔ ＋ Ｃｔ ３)
２
０
１
＋ ｔ － ２ ，０．５＜Ｈ（ｘ） ≤１
１ ＋ ｄｔ ＋ ｄｔ ＋ ｄｔ
１ ２ ３
— １ ５ ２ —
４