Page 34 - 2024年第55卷第12期

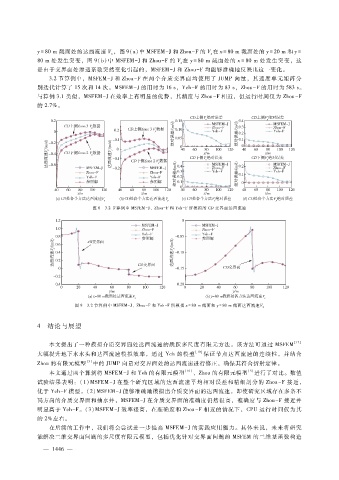
ｙ ＝ ８０ｍ截面处的达西流速 Ｖ，图 ９（ａ）中 ＭＳＦＥＭ－ Ｊ和 Ｚｈｏｕ － Ｆ的 Ｖ在 ｘ ＝ ８０ｍ截面处的 ｙ ＝ ２０ｍ和 ｙ ＝
ｘ ｘ
８０ｍ处发生突变，图 ９（ｂ）中 ＭＳＦＥＭ－ Ｊ和 Ｚｈｏｕ － Ｆ的 Ｖ在 ｙ ＝ ８０ｍ截面处的 ｘ ＝ ８０ｍ处发生突变，这
ｘ
是由于交界面处渗透系数突然变化引起的，ＭＳＦＥＭ－ Ｊ和 Ｚｈｏｕ － Ｆ均能够准确地反映出这一变化。
３．２节算例中，ＭＳＦＥＭ－ Ｊ和 Ｚｈｏｕ － Ｆ在两个介质交界面均使用了 ＪＵＭＰ向量，其速度单元矩阵分
别迭代计算了 １５次和 １４次。ＭＳＦＥＭ－ Ｊ的用时为 １６ｓ，Ｙｅｈ － Ｆ的用时为 ８３ｓ，Ｚｈｏｕ － Ｆ的用时为 ５８３ｓ。
与算例 ３．１类似，ＭＳＦＥＭ－ Ｊ在效率上有明显的优势，其精度与 Ｚｈｏｕ － Ｆ相近，但运行时间仅为 Ｚｈｏｕ － Ｆ
的 ２．７％。

图 ８ ３．２节算例中 ＭＳＦＥＭ－ Ｊ、Ｚｈｏｕ － Ｆ和 Ｙｅｈ － Ｆ所模拟的 ＣＤ交界面达西流速

图 ９ ３．２节算例中 ＭＳＦＥＭ－ Ｊ、Ｚｈｏｕ － Ｆ和 Ｙｅｈ － Ｆ所模拟 ｘ ＝ ８０ｍ截面和 ｙ ＝ ８０ｍ截面达西流速Ｖ ｘ

４ 结论与展望

本文提出了一种模拟介质交界面处达西流速的跳跃多尺度有限元方法。该方法可通过 ＭＳＦＥＭ ［１２］
大幅提升地下水水头和达西流速模拟效率，通过 Ｙｅｈ的模型 ［１０］ 保证节点达西流速的连续性，并结合
Ｚｈｏｕ的有限元模型 ［５］ 中的 ＪＵＭＰ向量对交界面处的达西流速进行修正，确保其符合折射定律。
本文通过两个算例将 ＭＳＦＥＭ－ Ｊ和 Ｙｅｈ的有限元模型 ［１０］ 、Ｚｈｏｕ的有限元模型 ［５］ 进行了对比。数值
试验结果表明：（ １）ＭＳＦＥＭ－ Ｊ在整个研究区域的达西流速平均相对误差和精细剖分的 Ｚｈｏｕ － Ｆ接近，
优于 Ｙｅｈ － Ｆ模型。（２）ＭＳＦＥＭ－ Ｊ能够准确地模拟出介质交界面的达西流速，即使研究区域存在多条不
同方向的介质交界面和抽水井，ＭＳＦＥＭ－ Ｊ在介质交界面的准确度仍然很高，准确度与 Ｚｈｏｕ － Ｆ接近并
明显高于 Ｙｅｈ － Ｆ。（３）ＭＳＦＥＭ－ Ｊ效率很高，在准确度和 Ｚｈｏｕ － Ｆ相近的情况下，ＣＰＵ运行时间仅为其
的 ２％左右。
在后续的工作中，我们将会尝试进一步提高 ＭＳＦＥＭ－ Ｊ的实践应用能力。具体来说，未来将研究
能解决三维交界面问题的多尺度有限元模型，包括优化针对交界面问题的 ＭＳＦＥＭ 的三维基函数构造

４
— １ ４ ６ —